Despite recent advances and press regarding the field, quantum computing is still veiled in mystery and myth, even within the field of data science and technology. Even those within the field of quantum computing and quantum machine learning are still learning the potential for progress and the stark limitations of current systems. However, quantum computing has arrived in its infancy, and many major companies are pouring money into related R&D efforts. D-Wave’s system has been commercially available for a couple of years already (albeit at a price tag of $10 million), and other systems have been opened for research purposes and commercial partnerships with quantum machine learning companies.
Quantum computing hardware theoretically can take on several different forms, each of which is suited to a different type of machine learning problem. However, in practice, two types of models are emerging as the dominant forms that quantum hardware are adhering to.
One of these involves qubit-based computational models, which replace classical bits with a quantum version of the bit (see image below). This means that qubits can exist in many different states, and be evolved into a final, optimized state.
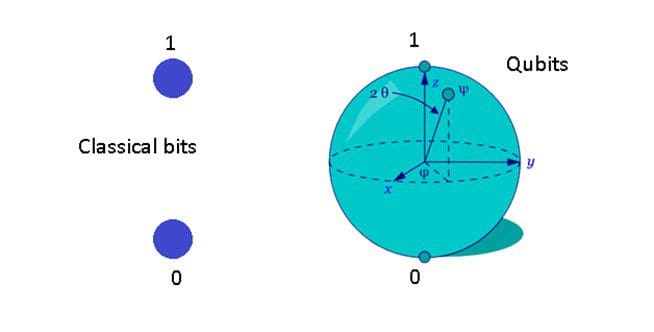
Two types of qubit chipsets exist—a chipset for quantum annealing processes and a gate-based circuits that extend the notion of classical chipsets. Both rely on quantum properties like superposition to speed up computation and improve accuracy. Qubit chipsets for quantum annealing rely on changing fields (i.e. – magnetic fields) to act on qubit states (D-Wave’s system), whereas gate-based circuits rely on gate operations to act on qubit states (IBM and Rigetti systems). While the performance of quantum-annealing-based designs are hard to benchmark, gate-based designs have been shown to speed up algorithms like Shor’s algorithm. Both types are available to quantum machine learning researchers. However, it is typically easier to access these through simulation software, which is implemented mainly in Python; this allows researchers to see how algorithms and software systems would work on the actual hardware and allows for easy integration with classical pipelines in Python.
The other dominant model of quantum computing is the qumodes-based circuit, which is the main focus on Xanadu’s hardware development. These leverage wave functions (specifically, photons), which are continuous probability distributions that can be squeezed, mapped, or otherwise operated on geometrically. A full hardware has yet to be completed, but Python’s Strawberry Fields software allows researchers to simulate qumode circuits and design algorithms for this type of quantum computer. Thus far, simulations are limited to 4 predictors and 1 outcome, with best performance coming from a small range of values taken by the predictors and outcome (generally within the -3 to 3 range).
In practice, execution of either qubit- or qumode-based design is difficult, as the quantum nature of these circuits introduces random error (as quantum mechanics is probabilistic in nature), interaction effects between particles (creating fields that can influence particle behavior), and tunneling behavior (where a particle escapes a barrier as a result of random fluctuations of a particle’s energy). Qubit systems to date also require extensive cooling systems for core processes, which results in very large machines with very specific needs; qumode systems do not require cooling but introduce other difficulties related to working with photons. All of these pose challenges to scaling quantum systems, qubit systems in particular. Because data is represented by the particles themselves in the physical system, this limits the size of data compatible with quantum computing and quantum machine learning to date. Most systems are under 64 qubits, though some 120+ qubit systems are slated for release in 2019.
However, the systems and simulation programs that exist are sufficient for researchers to explore potential algorithms and quantum versions of familiar machine learning models. In fact, prototypes of many common algorithms exist on these systems: deep learning, clustering, graph partitioning, shortest path algorithms, boosted regression, and even statistical models like generalized linear models. However, designing these algorithms and programming them requires not only a strong background in math and programming but also a strong enough background in quantum physics to design the circuits correctly. For those who have a solid foundation in these three areas, quantum machine learning can provide many advantages, as the mathematics of the model can be matched to the quantum circuit and operations, much as the XGBoost algorithm does on classical systems. Related open-source publications regarding quantum machine learning are listed in the reference section.
Many problems are well-suited for quantum computing, including graph theoretic algorithms (min flow/max cut, minimum coloring, clique-finding…–min flow/max cut example shown below), Bayesian algorithms, combinatorics problems like the one shown below (traveling salesman problems, encryption…), and even topological data analysis (persistent homology, homotopy continuation…). In addition, model geometry can be synergistically matched to the quantum mechanics underlying the circuit, as was done in the recent development of quantum generalized linear models, which eliminate the need for a link function (https://www.slideshare.net/ColleenFarrelly/quantum-generalized-linear-models). Researchers and data scientists focusing on those areas may want to take advantage of open-source papers regarding quantum hardware and quantum algorithms that have been designed in their area of expertise. Many opportunities exist for further development.

Quantum computing and quantum machine learning are still in their infancy. However, the field is rapidly developing, and advances in hardware design and algorithm development are open to interested researchers in industry and academia. It’s likely that commercially-available quantum computers will drop in price and find more uses in certain industries and companies within the next 5-10 years, and the field of quantum machine learning is widely open to innovation and guidance in its development.
References:
Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., & Lloyd, S. (2017). Quantum machine learning. Nature, 549(7671), 195.
Coecke, B., &Spekkens, R. W. (2012). Picturing classical and quantum Bayesian inference. Synthese, 186(3), 651-696.
Cui, S. X., Freedman, M. H., Sattath, O., Stong, R., & Minton, G. (2016). Quantum max-flow/min-cut. Journal of Mathematical Physics, 57(6), 062206.
Izaac, J., Quesada, N., Bergholm, V., Amy, M., &Weedbrook, C. (2018). Strawberry Fields: A Software Platform for Photonic Quantum Computing. arXiv preprint arXiv:1804.03159.
Lloyd, S., Garnerone, S., &Zanardi, P. (2016). Quantum algorithms for topological and geometric analysis of data. Nature communications, 7, 10138.
Orus, R., Mugel, S., &Lizaso, E. (2018). Quantum computing for finance: overview and prospects. arXiv preprint arXiv:1807.03890.
Pakin, S., & Reinhardt, S. P. (2018, June). A Survey of Programming Tools for D-Wave Quantum-Annealing Processors. In International Conference on High Performance Computing (pp. 103-122). Springer, Cham.
Rebentrost, P., Schuld, M., Wossnig, L., Petruccione, F., & Lloyd, S. (2016). Quantum gradient descent and Newton’s method for constrained polynomial optimization. arXiv preprint arXiv:1612.01789.
Rebentrost, P., Steffens, A., Marvian, I., & Lloyd, S. (2018). Quantum singular-value decomposition of nonsparse low-rank matrices. Physical review A, 97(1), 012327.
Wittek, P. (2014). Quantum machine learning: what quantum computing means to data mining. Academic Press
Related: