We have previously had a long look at a number of introductory natural language processing (NLP) topics, from approaching such tasks, to preprocessing text data, to getting started with a pair of popular Python libraries, and beyond. I was hoping to move on to exploring some different types of NLP tasks, but had it pointed out to me that I had neglected to touch on a hugely important aspect: data representation for natural language processing.
Just as in other types of machine learning tasks, in NLP we must find a way to represent our data (a series of texts) to our systems (e.g. a text classifier). As Yoav Goldberg asks, “How can we encode such categorical data in a way which is amenable for us by a statistical classifier?” Enter the word vector.
First, beyond “turning words into a numeric representation,” what are we interested in doing while we perform this data encoding? More precisely, what is it that we are encoding?
We must go from a set of categorical features in raw (or preprocessed) text – words, letters, POS tags, word arrangement, word order, etc. – to a series of vectors. Two options for achieving this encoding of textual data are sparse vectors (or one-hot encodings) and dense vectors.
These 2 approaches differ in a few fundamental ways. Read on for a discussion.
One-hot Encodings
Prior to the wide-spread use of neural networks in NLP – in what we will refer to as “traditional” NLP – vectorization of text often occurred via one-hot encoding (note that this persists as a useful encoding practice for a number of exercises, and has not fallen out of fashion due to the use of neural networks). For one-hot encoding, each word, or token, in a text corresponds to a vector element.
Source: Adrian Colyer
We could consider the image above, for example, as a small excerpt of a vector representing the sentence “The queen entered the room.” Note that only the element for “queen” has been activated, while those for “king,” “man,” etc. have not. You can imagine how differently the one-hot vector representation of the sentence “The king was once a man, but is now a child” would appear in the same vector element section pictured above.
The result of a one-hot encoding process on a corpus is a sparse matrix. Consider if you had a corpus with 20,000 unique words: a single short document in that corpus of, perhaps, 40 words would be represented by a matrix with 20,000 rows (one for each unique word) with a maximum of 40 non-zero matrix elements (and potentially far-fewer if there are a high number of non-unique words in this collection of 40 words). This leaves a lot of zeroes, and can end up taking a large amount of memory to house these spare representations.
Beyond potential memory capacity issues, a major drawback of one-hot encoding is the lack of meaning representation. While we capture the presence and absence of words in a particular text well with this approach, we can’t easily determine any meaning from simple presence/absence of these words. Part of this problem is that we lose positional relationships between words, or word order, using one-hot encoding. This order end up being paramount in representing meaning in words, and is addressed below.
The concept of word similarity is difficult to extract as well, since word vectors are statistically orthogonal. Take, for example, the word pairs “dog” and “dogs,” or “car” and “auto.” Clearly these word pair are similar in different ways, respectively. In a linear system, using one-hot encoding, traditional NLP tools such as stemming and lemmatization can be used in preprocessing to help expose the similarity between the first word pair; however, we need a more robust approach to tackle uncovering similarity between the second word pair.
The major benefit of one-hot encoded word vectors is that it captures binary word co-occurrence (it is alternately described as a bag of words), which is enough to perform a wide range of NLP tasks including text classification, one of the domain’s most useful and widespread pursuits. This type of word vector is useful for linear machine learning algorithms as well as neural networks, though they are most commonly associated with linear systems. Variants on one-hot encoding which are also useful to linear systems, and which help combat some of the above issues, are n-gram and TF-IDF representations. Though they are not the same as one-hot encoding, they are similar in that they are simple vector representations as opposed to embeddings, which are introduced below.
Dense Embedding Vectors
Sparse word vectors seem to be a perfectly acceptable way of representing certain text data in particular ways, especially considering binary word co-occurrence. We can also use related linear approaches to tackle some of the greatest and most obvious drawbacks of one-hot encodings, such as n-grams and TF-IDF. But getting tho the heart of the meaning of text, and the semantic relationship between tokens, remains difficult without taking a different approach, and word embedding vectors are just such an approach.
In “traditional” NLP, approaches such as manual or learned part-of-speech (POS) tagging can be used to determine which tokens in a text perform which types of function (noun, verb, adverb, indefinite article, etc.). This is a form of manual feature assignment, and these features can then be used for a variety of approaches to NLP functions. Consider, for example, named entity recognition: if we are looking for named entities within a passage of text, it would be reasonable to first look at only nouns (or noun phrases) in an attempt at identification, as named entities are almost exclusively a subset of all nouns.
However, let’s consider if we instead represented features as dense vectors – that is, with core features embedded into an embedding space of size d dimensions. We can compress, if you will, the number of dimensions used to represent 20,000 unique words down to, perhaps, 50 or 100 dimensions. In this approach, each feature no longer has its own dimension, and is instead mapped to a vector.
As stated earlier, it turns out that meaning is related not to binary word co-occurrence, but to word positional relationships. Think of it this way: if I say that the words “foo” and “bar” occur together in a sentence, determining meaning is difficult. However; if I say “The foo barked, which startled the young bar,” it becomes much easier to determine meanings of these words. The position of the words and their relationship to words around them are important.
“You shall know a word by the company it keeps.”
- John Rupert Firth
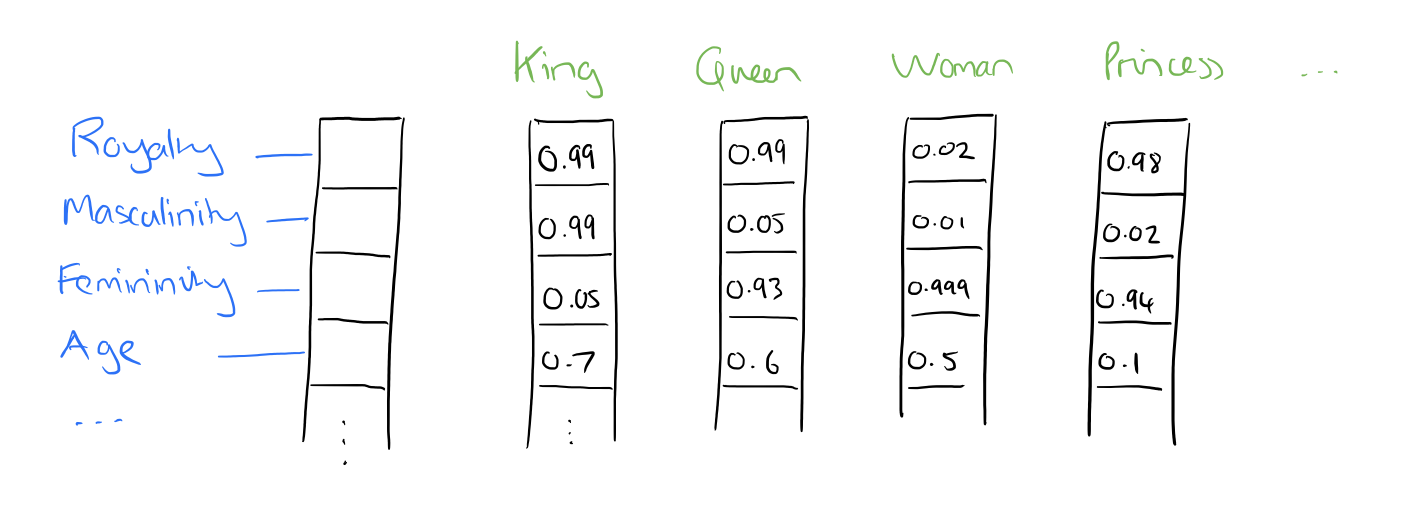Source: Adrian Colyer
So, what exactly are these features? We leave it to a neural network to determine the important aspects of relationships between words. Though human interpretation of these features would not be precisely possible, the image above provides an insight into what the underlying process may look like, relating to the famous King - Man + Woman = Queen example.
How are these features learned? This is accomplished by using a 2-layer (shallow) neural network – word embeddings are often grouped together with “deep learning” approaches to NLP, but the process of creating these embeddings does not use deep learning, though the learned weights are often used in deep learning tasks afterwords. The popular original word2vec embedding methods Continuous Bag of Words (CBOW) and Skip-gram relate to the tasks of predicting a word given its context, and predicting the context given a word (note that context is a sliding window of words in the text). We don’t care about the output layer of the model; it is discarded after training, and the weights of the embedding layer are then used for subsequent NLP neural network tasks. It is this embedding layers which is analogous to the resulting word vectors in the one-hot encoding approach.
There you have the 2 major approaches to representing text data for NLP tasks. We are now ready to have a look at some practical NLP tasks next time around.
References:
Natural Language Processing, National Research University Higher School of Economics (Coursera) Natural Language Processing, Yandex Data School Neural Network Methods for Natural Language Processing, Yoav Goldberg