As humans, we can quickly adapt our actions in new situations, be it recognizing objects from a few examples, or learning new skills and applying them in a matter of just a few minutes. But when it comes to deep learning techniques, an understandably large amount of time and data is required. So the challenge is to help our deep models do the same thing we can - to learn and quickly adapt from only a few examples, and to continue to adapt as more data becomes available. This approach of learning to learn is called meta-learning, and being a hot topic, has seen a flurry of research papers using techniques like matching networks, memory-augmented networks, sequence generative models, fast reinforcement learning and many others.
Meta-learning methods differ from many standard machine learning techniques, which involve training on a single task and testing on held-out examples from that task. These systems are trained by exposing them to a large number of tasks and are then tested in their ability to learn new tasks; an example of a task might be classifying a new image within 5 possible classes, given one example of each class.

A meta-learning set-up for few-shot image classification from a paper on Optimization as a Model for Few-Shot Learning
During this process, the model is trained to learn tasks in the meta-training set. There are two optimizations at play – the learner, which learns new tasks, and the meta-learner, which trains the learner.
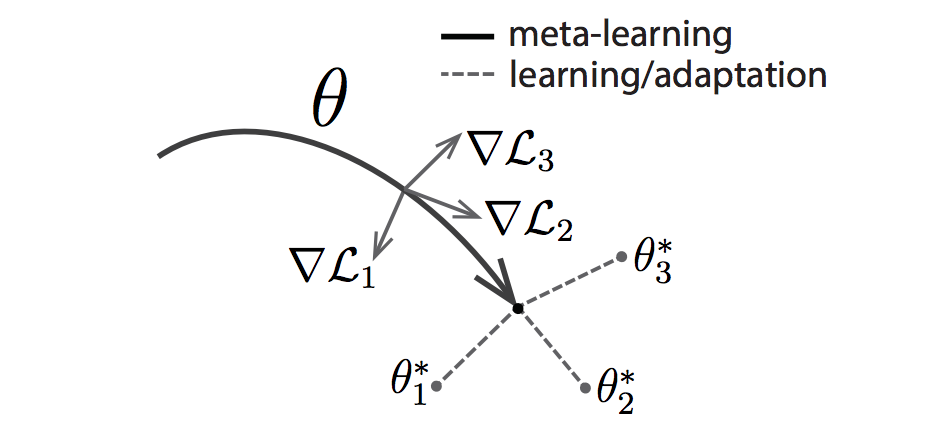
One of the recent benchmark papers in this area is MAML: Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. Like other meta-learning methods, MAML trains over a wide range of tasks. It trains for a representation that can be quickly adapted to a new task, via a few gradient steps. The meta-learner seeks to find an initialization that is not only useful for adapting to various problems, but also can be adapted quickly (in a small number of steps) and efficiently (using only a few examples). Suppose we are seeking to find a set of parameters θ that are highly adaptable. During the course of meta-learning (the bold line), MAML optimizes for a set of parameters such that when a gradient step is taken with respect to a particular task i (the gray lines), the parameters are close to the optimal parameters θ∗i for task i.
(image source)
This approach is quite simple and has some distinctive advantages:
It does not make any assumptions on the form of the model, in the sense that it can be applied to any learning problem and model trained with gradient descent procedure.
-
It is parameter efficient - there are no additional parameters introduced for meta-learning and the learner’s strategy uses a known optimization process (gradient descent), rather than having to come up with one from scratch.
-
And, unlike other approaches, it can be readily applied to classification, regression and reinforcement learning tasks.