This post gives a short overview of our recent paper:
BRUNO: A Deep Recurrent Model for Exchangeable Data by I. Korshunova, J. Degrave, F. Huszár, Y. Gal, A. Gretton, and J. Dambre
where we presented a provably exchangeable model whose:
-
predictive distribution is tractable to evaluate and can be sampled from with a linear complexity in the number of data points we condition on
-
training does not require variational approximations
-
memory complexity is constant thanks to its recurrent nature, i.e. after processing an observation we don’t have to store it in memory.
Motivation
We will give a two ways to motivate why BRUNO is an interesting model.
1. Exchangeability and Bayesian computations
We started from a problem posed in this inFERENCe blogpost: is it possible to design an exchangeable RNN? Ferenc explains it very well so please go ahead and read his blogpost. Below we will briefly repeat main definitions and how exchangeability is connected to Bayesian inference.
A sequence of random variables is said to be exchangeable if for all and all permutations
meaning that the joint probability remains the same under any permutation of the sequence.
Obviously, i.i.d. sequences are exchangeable. However, the converse is false: exchangeable sequences can be correlated.
One textbook example of an exchangeable sequence is a sequence of , which jointly has a multivariate normal distribution with a compound symmetry – or we will simply call it exchangeable – covariance structure:
where .
De Finetti’s theorem states that every exchangeable process – which is an infinite sequence of random variables – satisfies the following:
where is some parameter conditioned on which ’s become i.i.d.
In the Gaussian example above, one can show that are i.i.d. with conditioned on .
By conditioning both sides of Eq.1 on , de Finetti’s theorem can be written in terms of predictive distributions:
This is exactly the posterior predictive distribution, where we marginalised the likelihood of given with respect to the posterior distribution of . And here comes the thought: as long as our process is exchangeable, we can say that we do exact inference in some Bayesian model. We do not necessarily need to know what model is, but we know it exists! This is important as in what follows we will lose track of the underlying Bayesian model, but by maintaining the exchangeability property, we can be sure that there is one.
2. Meta-learning
Besides of Bayesian beauty, there is practical motivation for why we want to model exchangeable sequences. Many meta-learning problems can be framed as modelling unordered sets of objects which have some characteristic in common. For instance, in few-shot generative modelling, one might want to generate images that are somehow similar to the ones we’re already given.
In our paper, we demonstrated some examples of using exchangeable models on learning tasks that require generalisation from short unordered sequences while modelling sequence variability. Those applications include conditional image generation, few-shot classification, and set anomaly detection.
BRUNO model
Remember the example where and has an exchangeable structure? Essentially, this defines a very basic Gaussian process (GP) where its kernel is restricted to be exchangeable. As shown in the paper, this simplicity allows a) to derive recursive updates for the parameters of predictive distributions and b) to scale the process as instead of as in a common case.
While this clearly is an exchangeable model, it is way too simple to model complex observations, say when every is an image. Thus, we need some deep learning power. Namely, we are looking for a mapping from an intricate space to a simple latent space . Then in this simple space, one could indeed make use of exchangeable GPs. Such a mapping, however, has to be bijective (that’s why both and have to live in ). This would guarantee that exchangeable GP in space corresponds to some exchangeable process in space and the whole Bayesian reasoning of de Finetti holds for sequences in .
Luckily, there is a family of invertible neural nets architectures called Normalizing Flows that are used to transform simple densities into complex densities or the other way around. For our purpose, Real NVP suited most since a) its inverse mapping is fast to compute, which is useful when generating samples and b) computing the Jacobian is also fast, so we can quicky evaluate from using the change of variable formula:
Essentially, those are all the ingredients! A powerful bijection plus independent exchangeable GPs in the latent space make a nice exchangeable model which we called BRUNO: Bayesian RecUrrent Neural mOdel (TBH, we just wanted to name it after Bruno de Finetti). Here is a schematic:
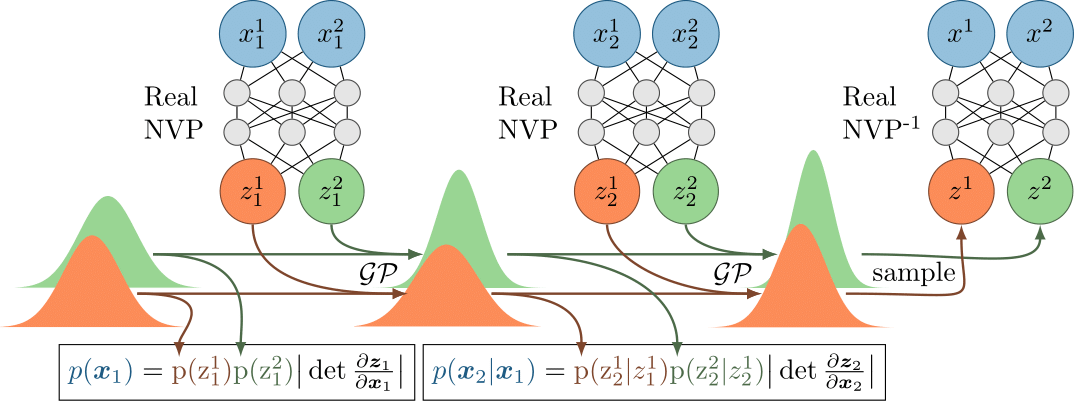
Because we have the predictive probabilities at every step, we can train BRUNO using MLE, where we maximise the likelihood of the inputs with respect to the Real NVP parameters and parameters of GPs kernels: and for every of the latent dimensions.
We train BRUNO on a dataset of i.i.d. sequences , where we assume that observations within a sequence are exchangeable. This assumption proved reasonable for sequences where observations belong to the same class. In this case, BRUNO should learn some class-specific features and also learn that those are correlated across the sequence. It appears to work well for the tasks of few-shot generation and classification, which we will look into next.
Experiments
Omniglot has become a standard dataset for testing few-shot learning algorithms. It is commonly referred to as the “transpose” of MNIST since it has a large number of character classes with only 20 examples per class. So if we train BRUNO on the same-class sequences from Omniglot’s train set, we can easily test its few-shot performance on the unseen characters.
Below are a few examples of generated samples conditionally on an input sequence of unseen characters. The cool thing about BRUNO is that it doesn’t need any retraining on classes it has never seen. We just need to feed BRUNO a test sequence of an arbitrary length and get our n-shot generated images as a result of sampling from a conditional distribution .
An input sequence is shown in the top row and samples in the bottom 4 rows. Every column of the bottom subplot contains 4 samples from the predictive distribution conditioned on the input images up to and including that column. That is, the 1st column shows samples from the prior when no input image is given; the 2nd column shows samples from where is the 1st input image in the top row and so on.
We can use the very same model for image classification in a n-shot, k-way setup. From the test accuracies below, we see that BRUNO is doing okay, but not as good as Matching Nets. That’s no surprise since BRUNO was trained as a generative model and may have wasted a lot of statistical power on modelling aspects of the data which are irrelevant for the classification task. However, if we now finetune BRUNO with a discriminative objective, i.e. maximising the likelihood of correct labels in few-shot classification episodes, its performance becomes a lot better.
| Model | n=1,k=5 | n=5,k=5 | n=1,k=20 | n=5,k=20 |
|---|---|---|---|---|
| Matching Nets | 98.1% | 98.9% | 93.8% | 98.5% |
| BRUNO | 86.3% | 95.6% | 69.2% | 87.7% |
| BRUNO finetuned | 97.1% | 99.4% | 91.3% | 97.8% |
In the paper, we have a few other datasets also give an example on how BRUNO can be used for set anomaly detection in a stream of incoming data .
Conclusion
Exchangeability has only recently started gaining more attention in deep learning community and hopefully will go a long way. Latest works such as Deep Sets, Neural Statistician, Neural Processes achive permutation invariance with respect to the inputs by aggregating their features, e.g. taking the mean across the sequence. Compared to these models, BRUNO has a different flavour: we want our model to strictly fullfill the definition of an exchangeable process such that de Finetti’s theorem is invoked and we have our exact (albeit implicit) Bayesian inference carried out in the space of images. It sounds cool and it works well in practice, so we hope somebody might find it useful.
Code
Our code is available on github: github.com/IraKorshunova/bruno