||
A quick puzzle this week.
Your friend offers you a bet: Roll six dice, and if you get exactly four distinct numbers you win.
Question: would you accept this deal at even odds?
For example a roll of 1,2,3,6,3,6 would win but a 1,6,3,4,2,6 would be a loss.
WIN
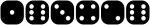LOSS
Give it a few minutes thought …
Solution
There are many ways to solve this. One of these is with brute force. There are only 46,656 possible combinations the dice can land on (6 × 6 × 6 × 6 × 6 × 6), and it’s just a couple of lines of code to write some nested loops and perform the check.
Here is a table showing the frequency count of every distinct combination of the spots.
| Distinct Count | Frequency | —— |
| 1 | 6 | |
| 2 | 930 | |
| 3 | 10,800 | |
| 4 | 23,400 | |
| 5 | 10,800 | |
| 6 | 720 | |
| TOTAL | 46,656 |
As you can see, the total number of combinations with a distinct count of four is 23,400/46,656 which simplifies to 325/648, which is just a little more than 50:50, so it’s (just) slightly better than even odds. Yes, it’s a good bet to take!
Yes, it’s a good bet.
Formal Solution
Solving with brute force might not be very elegant, but it’s simple to write. You could optimize a little from symmetry, but let’s apply logic and come up for a formal solution.
There are only two possible ways we can get a distinct count of four:
Three of a kind, then three distinct singletons.
Two (different) pairs, with two distinct singletons.
Triple
There are 6 possible values for what the triplet dice would be, and there are 6 choose 3 ways this triplet could appear. There are then 5 values that the first singleton could be, 4 values for the second, and 3 for the last singleton. This is 6 × 6C3 × 5 × 4 × 3 = 7,200 possible combinations.
7,200/46,656 = 25/162.
Two Pair
With two pairs, there are 6C2 for what these numbers are. The first pair has 6C2 choices of where to go, and the second pair has 4C2 choices of position. There are then 4 possible combinations for the first singleton, and 3 possible for the last singleton.
This is 6C2 × 6C2 × 4C2 × 4 × 3 = 15 × 15 × 6 × 4 × 3 = 16,200 possible combinations.
16,200/46,656 = 25/72.
Total
Adding these together, we get (7,200+16,200)/46,656 = 23,400/46,656 = 325/648
This confirms the answer we obtained from brute force! (Approx 50.15%)
You can find a complete list of all the articles here.
Click here to receive email alerts on new articles.