Two cool features of Python NumPy： Mutating by slicing and Broadcasting

Mutation by slicing

It turns out that if you use simple slicing/indexing with NumPy to create a sub-array, the sub-array actually points to the main array. Simply put, the in-memory diagram looks like,

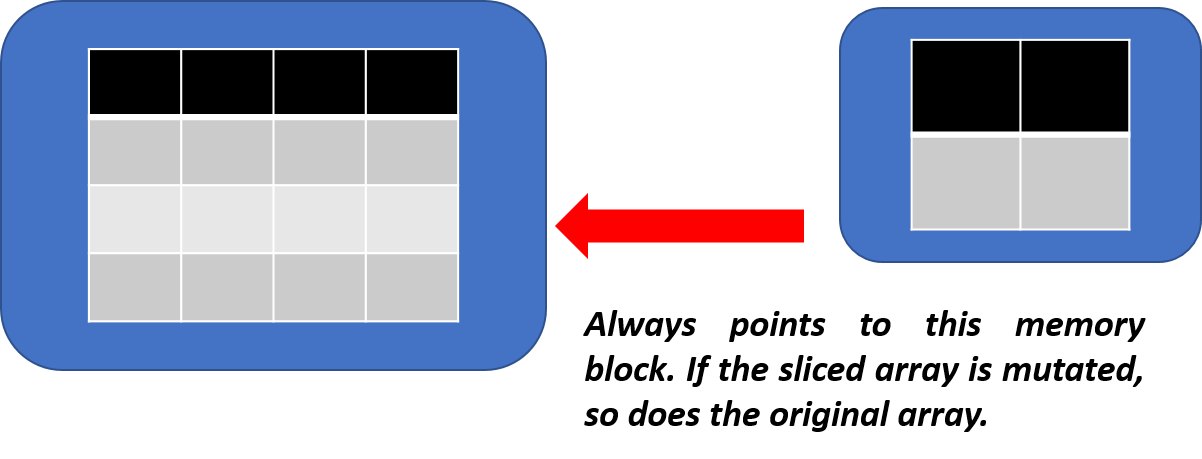
Therefore, if the sliced array is changed, it affects the parent array too. This could be a useful feature to propagate the desired chain up the food chain but sometimes could also be a nuisance where you to keep the main data set immutable and effect your changes on the subset only. In those cases, you have to explicitly call np.array method to define the sliced array, not just slice it out by indexing. The following code illustrates the point,

Illustrative code

mat = np.array([[11,12,13],[21,22,23],[31,32,33]])
print("Original matrix")
print(mat)

# Simple Indexing
mat_slice = mat[:2,:2]

print ("\nSliced matrix")
print(mat_slice)
print ("\nChange the sliced matrix")
mat_slice[0,0] = 1000
print (mat_slice)
print("\nBut the original matrix? WHOA! It got changed too!")
print(mat)

The result looks like,

Original matrix
[[11 12 13]
 [21 22 23]
 [31 32 33]]

Sliced matrix
[[11 12]
 [21 22]]

Change the sliced matrix
[[1000 12]
 [21 22]]

But the original matrix? WHOA! It got changed too!
[[1000 12 13]
 [21 22 23]
 [31 32 33]]

To stop this from happening, this is what you should do,

# Little different way to create a copy of the sliced matrix
print ("\nDoing it again little differently now...\n")
mat = np.array([[11,12,13],[21,22,23],[31,32,33]])
print("Original matrix")
print(mat)

# Notice the np.array method
mat_slice = np.array(mat[:2,:2])

print ("\nSliced matrix")
print(mat_slice)
print ("\nChange the sliced matrix")
mat_slice[0,0] = 1000
print (mat_slice)
print("\nBut the original matrix? NO CHANGE this time:)")
print(mat)

Now the original matrix is not mutated by any change in the sub-matrix,

Original matrix
[[11 12 13]
 [21 22 23]
 [31 32 33]]

Sliced matrix
[[11 12]
 [21 22]]

Change the sliced matrix
[[1000 12]
 [21 22]]

But the original matrix? NO CHANGE this time:)
[[11 12 13]
 [21 22 23]
 [31 32 33]]

Broadcasting

NumPy operations are usually done on pairs of arrays on an element-by-element basis. In the general case, the two arrays must have exactly the same shape (or for matrix multiplication the inner dimension must conform).

NumPy’s broadcasting rule relaxes this constraint when the arrays’ shapes meet certain constraints. When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing dimensions, and works its way forward. Two dimensions are compatible when

they are equal, or
one of them is 1

If these conditions are not met, a ValueError: frames are not aligned exception is thrown, indicating that the arrays have incompatible shapes. The size of the resulting array is the maximum size along each dimension of the input arrays.

For more detail, please look up: https://docs.scipy.org/doc/numpy-1.10.1/user/basics.broadcasting.html.

Following code block illustrates the idea step-by-step,

Initialize a ‘start’ matrix with zeroes

start = np.zeros((4,3))
print(start)

[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

Create a row matrix (vector),

# create a rank 1 ndarray with 3 values
add_rows = np.array([1, 0, 2])
print(add_rows)

[1 0 2]

Add the zero-matrix (4x3) to the (1x3) vector. Automatically, the 1x3 vector is duplicated 4 times to match the row dimension of the zero matrix and those values are added to the 4x3 matrix.

y = start + add_rows # add to each row of 'start'
print(y)

[[1. 0. 2.]
 [1. 0. 2.]
 [1. 0. 2.]
 [1. 0. 2.]]

Create a column matrix (vector),

# create an ndarray which is 4 x 1 to broadcast across columns
add_cols = np.array([[0,1,2,3]])
add_cols = add_cols.T
print(add_cols)

[[0]
 [1]
 [2]
 [3]]

Add the zero-matrix (4x3) to the (4x1) vector. Automatically, the 4x1 vector is duplicated 3 times to match the column dimension of the zero matrix and those values are added to the 4x3 matrix.

# add to each column of 'start' using broadcasting
y = start + add_cols 
print(y)

[[0. 0. 0.]
 [1. 1. 1.]
 [2. 2. 2.]
 [3. 3. 3.]]

Finally, a scalar is treated like a 1x1 matrix and duplicated exactly to the size of the additive matrix to execute the operation.

# this will just broadcast in both dimensions
add_scalar = np.array([100]) 
print(start+add_scalar)

[[100. 100. 100.]
 [100. 100. 100.]
 [100. 100. 100.]
 [100. 100. 100.]]

Utility of broadcasting is best realized when you use NumPy arrays to write vectorized code for an algorithm like gradient descent. Andrew Ng spends a full video lecture explaining the concept of broadcasting in Python in his new Deep Learning course. It makes the implementation of the forward and back-propagation algorithm for deep neural network relatively painless.

You can check out this video also about demonstration of broadcasting feature…

Numpy Broadcasting explanation video

If you have any questions or ideas to share, please contact the author at tirthajyoti[AT]gmail.com. Also you can check author’s GitHub repositories for other fun code snippets in Python, R, or MATLAB and machine learning resources. You can also follow me on LinkedIn.