It’s Superbowl LII day today. Superbowls, clock-faces, and occasionally fancy documents still use Roman Numerals (along with Kings, Queens, Popes and the Olympic Games).
Here’s a quick geometry puzzle that you might like to knock-out during the half-time concert. It’s not too challenging once you see the trick that makes it easy.
In the diagram below (which is supposed to look like a football helmet), an equilateral triangle with a side length of the diameter, is overlaid over the circle so that it passes through the centre of the circle. The question is to determine the area of the shaded region.
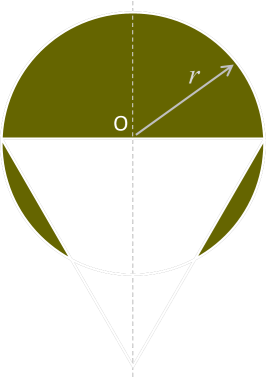
What is the area of the shaded region?
Solution Have a quick think, then click the button below to reveal the solution.
Answer
The easiest thing to do it break it down into components.
What we need to calculate now is the area of the two side ‘chops’.
Here’s the trick that makes it easy. In the diagram below we can see the two coloured regions, combined, form the segment which is 1/6th the area of the circle (which is easy to determine). To get the area of the ‘chop’ all we have to do is subtract away the area of the smaller equilateral triangle. There are two ‘chops’ in the shaded space.
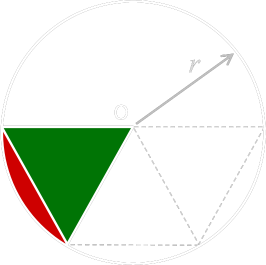
The formula for the area of an equilateral triangle, based on length of a side, is well known (and easy to derive). The side of the smaller triangle, is just the radius r.
(Close to 56% of the area of the circle).
You can find a complete list of all the articles here.
Click here to receive email alerts on new articles.