Using regression trees for forecasting double-seasonal time series with trend in R

转载自：https://petolau.github.io/Regression-trees-for-forecasting-time-series-in-R/

未知
发表于

After blogging break caused by writing research papers, I managed to secure time to write something new about time series forecasting. This time I want to share with you my experiences with seasonal-trend time series forecasting using simple regression trees. Classification and regression tree (or decision tree) is broadly used machine learning method for modeling. They are favorite because of these factors:

  • simple to understand (white box)

  • from a tree we can extract interpretable results and make simple decisions

  • they are helpful for exploratory analysis as binary structure of tree is simple to visualize

  • very good prediction accuracy performance

  • very fast

  • they can be simply tuned by ensemble learning techniques

But! There is always some “but”, they poorly adapt when new unexpected situations (values) appears. In other words, they can not detect and adapt to change or concept drift well (absolutely not). This is due to the fact that tree creates during learning just simple rules based on training data. Simple decision tree does not compute any regression coefficients like linear regression, so trend modeling is not possible. You would ask now, so why we are talking about time series forecasting with regression tree together, right? I will explain how to deal with it in more detail further in this post.

You will learn in this post how to:

  • decompose double-seasonal time series

  • detrend time series

  • model and forecast double-seasonal time series with trend

  • use two types of simple regression trees

  • set important hyperparameters related to regression tree

Exploring time series data of electricity consumption

As in previous posts, I will use smart meter data of electricity consumption for demonstrating forecasting of seasonal time series. I created a new dataset of aggregated electricity load of consumers from an anonymous area. Time series data have the length of 17 weeks.

Firstly, let’s scan all of the needed packages for data analysis, modeling and visualizing.

1
2
3
4
5
6
7
8
9
10
11
library(feather) # data import
library(data.table) # data handle
library(rpart) # decision tree method
library(rpart.plot) # tree plot
library(party) # decision tree method
library(forecast) # forecasting methods
library(ggplot2) # visualizations
library(ggforce) # visualization tools
library(plotly) # interactive visualizations
library(grid) # visualizations
library(animation) # gif

Now read the mentioned time series data by read_feather to one data.table. The dataset can be found on my github repo, the name of the file is DT_load_17weeks.

DT <- as.data.table(read_feather(“DT_load_17weeks”))

1
2
3

And store information of the date and period of time series that is 48.

n_date <- unique(DT[, date]) period <- 48

1
2
3

For data visualization needs, store my favorite ggplot theme settings by function `theme`.

theme_ts <- theme(panel.border = element_rect(fill = NA, colour = “grey10”), panel.background = element_blank(), panel.grid.minor = element_line(colour = “grey85”), panel.grid.major = element_line(colour = “grey85”), panel.grid.major.x = element_line(colour = “grey85”), axis.text = element_text(size = 13, face = “bold”), axis.title = element_text(size = 15, face = “bold”), plot.title = element_text(size = 16, face = “bold”), strip.text = element_text(size = 16, face = “bold”), strip.background = element_rect(colour = “black”), legend.text = element_text(size = 15), legend.title = element_text(size = 16, face = “bold”), legend.background = element_rect(fill = “white”), legend.key = element_rect(fill = “white”))

1
2
3

Now, pick some dates of the length 3 weeks from dataset to split data on the train and test part. Test set has the length of only one day because we will perform one day ahead forecast of electricity consumption.

data_train <- DT[date %in% n_date[43:63]] data_test <- DT[date %in% n_date[64]]

1
2
3

Let’s plot the train set and corresponding average weekly values of electricity load.

averages <- data.table(value = rep(sapply(0:2, function(i) mean(data_train[((iperiod7)+1):((i+1)period7), value])), each = period * 7), date_time = data_train$date_time)

ggplot(data_train, aes(date_time, value)) + geom_line() + geom_line(data = averages, aes(date_time, value), linetype = 5, alpha = 0.75, size = 1.2, color = “firebrick2”) + labs(x = “Date”, y = “Load (kW)”) + theme_ts

1
2
3
4
5
6
7
8
9
10
11

![](https://petolau.github.io/images/post_5/unnamed-chunk-7-1.png)


We can see some trend increasing over time, maybe air conditioning is more used when gets hotter in summer. The double-seasonal (daily and weekly) character of time series is obvious.

A very useful method for visualization and analysis of time series is STL decomposition.
STL decomposition is based on Loess regression, and it decomposes time series to three parts: seasonal, trend and remainder.
We will use results from the STL decomposition to model our data as well.
I am using `stl()` from `stats` package and before computation we must define weekly seasonality to our time series object. Let’s look on results:

data_ts <- ts(data_train$value, freq = period * 7) decomp_ts <- stl(data_ts, s.window = “periodic”, robust = TRUE)$time.series

decomp_stl <- data.table(Load = c(data_train$value, as.numeric(decomp_ts)), Date = rep(data_train[,date_time], ncol(decomp_ts)+1), Type = factor(rep(c(“original data”, colnames(decomp_ts)), each = nrow(decomp_ts)), levels = c(“original data”, colnames(decomp_ts))))

ggplot(decomp_stl, aes(x = Date, y = Load)) + geom_line() + facet_grid(Type ~ ., scales = “free_y”, switch = “y”) + labs(x = “Date”, y = NULL, title = “Time Series Decomposition by STL”) + theme_ts

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

![](https://petolau.github.io/images/post_5/unnamed-chunk-8-1.png)


As was expected from the previous picture, we can see that there is “slight” trend increasing and decreasing (by around 100 kW so slightly large ;) ).
Remainder part (noise) is very fluctuate and not seems like classical white noise (we obviously missing additional information like weather and other unexpected situations).

## Constructing features to model

In this section I will do **feature engineering** for modeling double-seasonal **time series** with trend best as possible by just available historical values.

Classical way to handle seasonality is to add seasonal features to a model as vectors of form \( (1, \dots, DailyPeriod, 1, …, DailyPeriod,…) \) for daily season or \( (1, \dots, 1, 2, \dots, 2, \dots , 7, 1, \dots) \) for weekly season. I used it this way in my previous post about GAM and somehow similar also with multiple linear regression.

A better way to model seasonal variables (features) with **nonlinear regression** methods like **tree** is to transform it to Fourier terms (sinus and cosine). It is more effective to tree models and also other nonlinear machine learning methods. I will explain why it is like that further of this post.

Fourier daily signals (terms) are defined as:

where \( ds \) is number of daily seasonality Fourier pairs and Fourier weekly terms are defines as:

where \( ws \) is a number of weekly seasonality Fourier pairs.

Another great feature (most of the times most powerful) is a lag of original time series. We can use lag by one day, one week, etc…
The lag of time series can be preprocessed by removing noise or trend for example by STL decomposition method to ensure stability.

As was earlier mentioned, regression trees can’t predict trend because they logically make rules and predict future values only by rules made by training set.
Therefore original time series that inputs to regression tree as dependent variable must be detrended (removing the trend part of the time series). The acquired trend part then can be forecasted by for example ARIMA model.

Let’s go to constructing mentioned features and trend forecasting.

Double-seasonal Fourier terms can be simply extracted by `fourier` function from `forecast` package.
Firstly, we must create multiple seasonal object with function `msts`.

data_msts <- msts(data_train$value, seasonal.periods = c(period, period*7))

Now use fourier function using two conditions for a number of K terms. Set K for example just to 2.

1
2
K <- 2
fuur <- fourier(data_msts, K = c(K, K))

It made 2 pairs (sine and cosine) of daily and weekly seasonal signals. If we compare it with approach described in previous posts, so simple periodic vectors, it looks like this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Daily <- rep(1:period, 21) # simple daily vector
Weekly <- data_train[, week_num] # simple weekly vector
 
data_fuur_simple <- data.table(value = c(scale(Daily), fuur[,2], scale(Weekly), fuur[,6]),
 date = rep(data_train$date_time, 4),
 method = rep(c("simple-daily", "four-daily",
 "simple-weekly", "four-weekly"),
 each = nrow(fuur)),
 type = rep(c("Daily season", "Weekly season"),
 each = nrow(fuur)*2))
 
ggplot(data_fuur_simple, aes(x = date, y = value, color = method)) +
 geom_line(size = 1.2, alpha = 0.7) + 
 facet_grid(type ~ ., scales = "free_y", switch = "y") +
 labs(x = "Date", y = NULL,
 title = "Features Comparison") +
 theme_ts

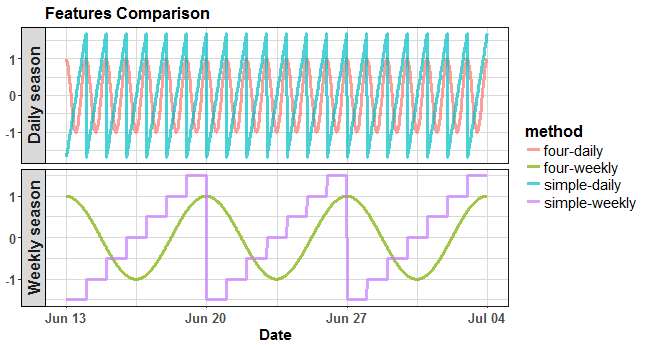
where four-daily is the Fourier term for daily season, simple-daily is the simple feature for daily season, four-weekly is the Fourier term for weekly season, and simple-weekly is the simple feature for weekly season. The advantage of Fourier terms is that there is much more closeness between ending and starting of a day or a week, which is more natural.

Now, let’s use data from STL decomposition to forecast trend part of time series. I will use auto.arima procedure from the forecast package to perform this.

1
2
3
trend_part <- ts(decomp_ts[,2])
trend_fit <- auto.arima(trend_part)
trend_for <- forecast(trend_fit, period)$mean

Let’s plot it:

1
2
3
4
5
6
7
8
9
trend_data <- data.table(Load = c(decomp_ts[,2], trend_for),
 Date = c(data_train$date_time, data_test$date_time),
 Type = c(rep("Real", nrow(data_train)), rep("Forecast",
 nrow(data_test))))
 
ggplot(trend_data, aes(Date, Load, color = Type)) +
 geom_line(size = 1.2) +
 labs(title = paste(trend_fit)) +
 theme_ts

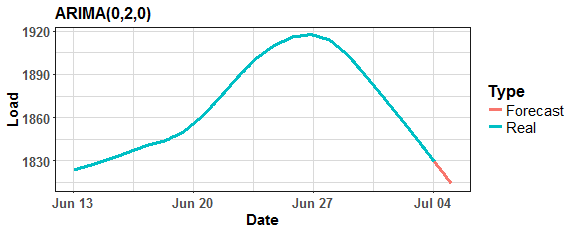
Function auto.arima chose ARIMA(0,2,0) model as best for trend forecasting.

Next, make the final feature to the model (lag) and construct train matrix (model matrix). I am creating lag by one day and just taking seasonal part from STL decomposition (for having smooth lag time series feature).

1
2
3
4
5
6
7
8
9
N <- nrow(data_train)
window <- (N / period) - 1 # number of days in train set minus lag
 
new_load <- rowSums(decomp_ts[, c(1,3)]) # detrended load
lag_seas <- decomp_ts[1:(period*window), 1] # seasonal part of time series as lag feature
 
matrix_train <- data.table(Load = tail(new_load, window*period),
 fuur[(period + 1):N,],
 Lag = lag_seas)

The accuracy of forecast (or fitted values of a model) will be measured by MAPE, let’s defined it:

1
2
3
mape <- function(real, pred){
 return(100 * mean(abs((real - pred)/real))) # MAPE - Mean Absolute Percentage Error
}

RPART (CART) tree

In the next two sections, I will describe two regression tree methods. The first is RPART, or CART (Classification and Regression Trees), the second will be CTREE. RPART is recursive partitioning type of binary tree for classification or regression tasks. It performs a search over all possible splits by maximizing an information measure of node impurity, selecting the covariate showing the best split.

I’m using rpart implementation from the same named package. Let’s go forward to modeling and try default settings of rpart function:

tree_1 <- rpart(Load ~ ., data = matrix_train)

1
2
3
4
5

It makes many interesting outputs to check, for example we can see a table of nodes and corresponding errors by `printcp(tree_1)` or see a detailed summary of created nodes by `summary(tree_1)`. We will check variable importance and number of created splits:

tree_1$variable.importance

Lag C2-48 C1-336 S1-48 C1-48 S1-336 C2-336

100504751 45918330 44310331 36245736 32359598 27831258 25385506

S2-336 S2-48

15156041 7595266

paste(“Number of splits: “, tree_1$cptable[dim(tree_1$cptable)[1], “nsplit”])

[1] “Number of splits: 10”

1
2
3
4
5

We can see that most important variables are Lag and cosine forms of the daily and weekly season. The number of splits is 10, ehm, is it enough for time series of length 1008 values?

Let’s plot created rules with fancy `rpart.plot` function from the same named package:

rpart.plot(tree_1, digits = 2, box.palette = viridis::viridis(10, option = “D”, begin = 0.85, end = 0), shadow.col = “grey65”, col = “grey99”)

1
2
3
4
5
6
7
8

![](https://petolau.github.io/images/post_5/unnamed-chunk-18-1.png)


We can see values, rules, and percentage of values split each time. Pretty simple and interpretable.

Now plot fitted values to see results of the `tree_1` model.

datas <- data.table(Load = c(matrix_train$Load, predict(tree_1)), Time = rep(1:length(matrix_train$Load), 2), Type = rep(c(“Real”, “RPART”), each = length(matrix_train$Load)))

ggplot(datas, aes(Time, Load, color = Type)) + geom_line(size = 0.8, alpha = 0.75) + labs(y = “Detrended load”, title = “Fitted values from RPART tree”) + theme_ts

1
2
3
4
5
6
7
8
9

![](https://petolau.github.io/images/post_5/unnamed-chunk-19-1.png)


And see the error of fitted values against real values.

mape(matrix_train$Load, predict(tree_1))

## [1] 180.6669

Whups. It’s a little bit simple (rectangular) and not really accurate, but it’s logical result from a simple tree model. The key to achieving better results and have more accurate fit is to set manually control hyperparameters of rpart. Check ?rpart.control to get more information. The “hack” is to change cp (complexity) parameter to very low to produce more splits (nodes). The cp is a threshold deciding if each branch fulfills conditions for further processing, so only nodes with fitness larger than factor cp are processed. Other important parameters are the minimum number of observations in needed in a node to split (minsplit) and the maximal depth of a tree (maxdepth). Set the minsplit to 2 and set the maxdepth to its maximal value - 30.

1
2
3
4
tree_2 <- rpart(Load ~ ., data = matrix_train,
 control = rpart.control(minsplit = 2,
 maxdepth = 30,
 cp = 0.000001))

Now make simple plot to see depth of the created tree…

plot(tree_2, compress = TRUE)

1
2
3
4
5
6
7
8
9
10

![](https://petolau.github.io/images/post_5/unnamed-chunk-22-1.png)


That’s little bit impressive difference than previous one, isn’t it?
Check also number of splits.

tree_2$cptable[dim(tree_2$cptable)[1], "nsplit"] # Number of splits

## [1] 600

600 is higher than 10 :)

Let’s plot fitted values from the model tree_2:

1
2
3
4
5
6
7
8
9
datas <- data.table(Load = c(matrix_train$Load,
 predict(tree_2)),
 Time = rep(1:length(matrix_train$Load), 2),
 Type = rep(c("Real", "RPART"), each = length(matrix_train$Load)))
 
ggplot(datas, aes(Time, Load, color = Type)) +
 geom_line(size = 0.8, alpha = 0.75) +
 labs(y = "Detrended load", title = "Fitted values from RPART") +
 theme_ts

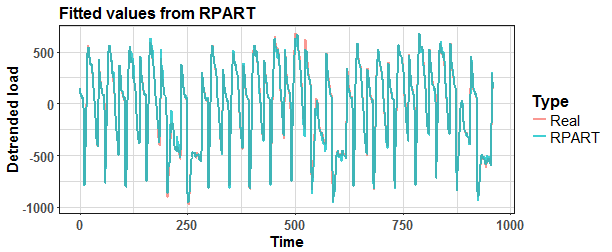
And see the error of fitted values against real values.

mape(matrix_train$Load, predict(tree_2))

[1] 16.0639

1
2
3
4
5
6

Much better, but obviously the model can be overfitted now.

Add together everything that we got till now, so forecast load one day ahead.
Let’s create testing data matrix:

test_lag <- decomp_ts[((period*window)+1):N, 1] fuur_test <- fourier(data_msts, K = c(K, K), h = period)

matrix_test <- data.table(fuur_test, Lag = test_lag)

1
2
3
4

Predict detrended time series part with `tree_2` model + add the trend part of time series forecasted by ARIMA model.

for_rpart <- predict(tree_2, matrix_test) + trend_for

Let’s plot the results and compare it with real values from data_test.

1
2
3
4
5
6
7
8
9
10
11
data_for <- data.table(Load = c(data_train$value, data_test$value, for_rpart),
 Date = c(data_train$date_time, rep(data_test$date_time, 2)),
 Type = c(rep("Train data", nrow(data_train)),
 rep("Test data", nrow(data_test)),
 rep("Forecast", nrow(data_test))))
 
ggplot(data_for, aes(Date, Load, color = Type)) +
 geom_line(size = 0.8, alpha = 0.75) +
 facet_zoom(x = Date %in% data_test$date_time, zoom.size = 1.2) +
 labs(title = "Forecast from RPART") +
 theme_ts

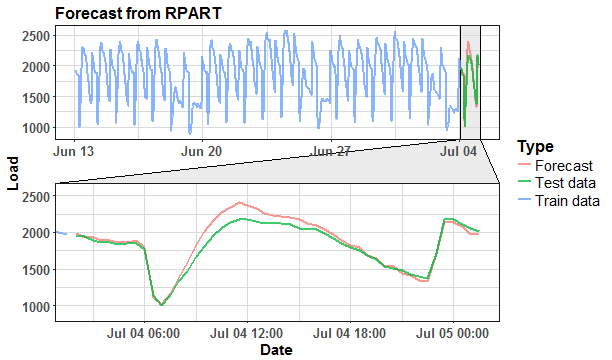
Not bad. For clarity, compare forecasting results with model without separate trend forecasting and detrending.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
matrix_train_sim <- data.table(Load = tail(data_train$value, window*period),
 fuur[(period+1):N,],
 Lag = lag_seas)
 
tree_sim <- rpart(Load ~ ., data = matrix_train_sim,
 control = rpart.control(minsplit = 2,
 maxdepth = 30,
 cp = 0.000001))
for_rpart_sim <- predict(tree_sim, matrix_test)
 
data_for <- data.table(Load = c(data_train$value, data_test$value, for_rpart, for_rpart_sim),
 Date = c(data_train$date_time, rep(data_test$date_time, 3)),
 Type = c(rep("Train data", nrow(data_train)),
 rep("Test data", nrow(data_test)),
 rep("Forecast with trend", nrow(data_test)),
 rep("Forecast simple", nrow(data_test))))
 
ggplot(data_for, aes(Date, Load, color = Type, linetype = Type)) +
 geom_line(size = 0.8, alpha = 0.7) +
 facet_zoom(x = Date %in% data_test$date_time, zoom.size = 1.2) +
 labs(title = "Forecasts from RPARTs with and without trend forecasting") +
 scale_linetype_manual(values = c(5,6,1,1)) +
 theme_ts

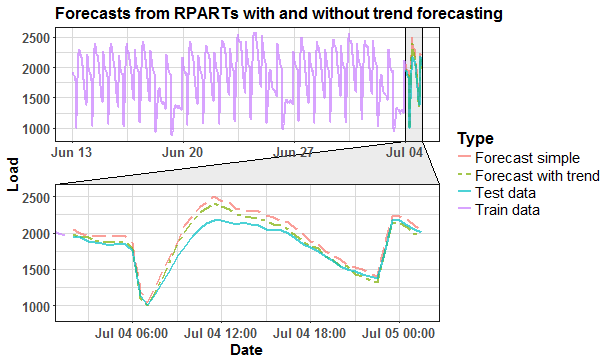
We can see that RPART model without trend manipulation has higher values of the forecast. Evaluate results with MAPE forecasting measure.

mape(data_test$value, for_rpart)

[1] 3.727473

mape(data_test$value, for_rpart_sim)

[1] 6.976259

1
2
3
4
5
6
7
8
9
10
11

We can see the large difference in MAPE. So detrending original time series and forecasting separately trend part really works, but not generalize the result now. You can read more about RPART method in its great package vignette.

## CTREE

The second simple regression tree method that will be used is **CTREE**. Conditional inference trees (CTREE) is a statistical approach to recursive partitioning, which takes into account the distributional properties of the data. CTREE performs multiple test procedures that are applied to determine whether no significant association between any of the feature and the response (load in the our case) can be stated and the recursion needs to stop.
In **R** CTREE is implemented in the package `party` in the function `ctree`.

Let’s try fit simple `ctree` with a default values.

ctree_1 <- ctree(Load ~ ., data = matrix_train)

Constructed tree can be again simply plotted by plot function, but it made many splits so it’s disarranged.

Let’s plot fitted values from ctree_1 model.

1
2
3
4
5
6
7
8
9
datas <- data.table(Load = c(matrix_train$Load,
 predict(ctree_1)),
 Time = rep(1:length(matrix_train$Load), 2),
 Type = rep(c("Real", "CTREE"), each = length(matrix_train$Load)))
 
ggplot(datas, aes(Time, Load, color = Type)) +
 geom_line(size = 0.8, alpha = 0.75) +
 labs(y = "Detrended load", title = "Fitted values from CTREE") +
 theme_ts

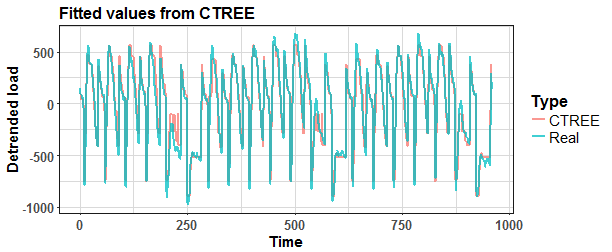
And see the error of fitted values against real values.

mape(matrix_train$Load, predict(ctree_1))

[1] 87.85983

1
2
3
4
5

Actually, this is pretty nice, but again, it can be tuned.

For available hyperparameters tuning check `?ctree_control`. I changed hyperparameters `minsplit` and `minbucket` that have similar meaning like the cp parameter in RPART. The `mincriterion` can be tuned also, and it is significance level (1 - p-value) that must be exceeded in order to implement a split. Let’s plot results.

ctree_2 <- ctree(Load ~ ., data = matrix_train, controls = party::ctree_control(teststat = “quad”, testtype = “Teststatistic”, mincriterion = 0.925, minsplit = 1, minbucket = 1))

datas <- data.table(Load = c(matrix_train$Load, predict(ctree_2)), Time = rep(1:length(matrix_train$Load), 2), Type = rep(c(“Real”, “CTREE”), each = length(matrix_train$Load)))

ggplot(datas, aes(Time, Load, color = Type)) + geom_line(size = 0.8, alpha = 0.75) + labs(y = “Detrended load”, title = “Fitted values from CTREE”) + theme_ts

1
2
3
4
5
6
7
8
9

![](https://petolau.github.io/images/post_5/unnamed-chunk-34-1.png)


And see the error of fitted values against real values.

mape(matrix_train$Load, predict(ctree_2))

## [1] 39.70532

It’s better. Now forecast values with ctree_2 model.

for_ctree <- predict(ctree_2, matrix_test) + trend_for

1
2
3

And compare CTREE with RPART model.

data_for <- data.table(Load = c(data_train$value, data_test$value, for_rpart, for_ctree), Date = c(data_train$date_time, rep(data_test$date_time, 3)), Type = c(rep(“Train data”, nrow(data_train)), rep(“Test data”, nrow(data_test)), rep(“RPART”, nrow(data_test)), rep(“CTREE”, nrow(data_test))))

ggplot(data_for, aes(Date, Load, color = Type, linetype = Type)) + geom_line(size = 0.8, alpha = 0.7) + facet_zoom(x = Date %in% data_test$date_time, zoom.size = 1.2) + labs(title = “Forecasts from RPART and CTREE models”) + scale_linetype_manual(values = c(5,6,1,1)) + theme_ts

1
2
3
4
5
6
7
8
9
10
11

![](https://petolau.github.io/images/post_5/unnamed-chunk-37-1.png)


mape(data_test$value, for_rpart)

## [1] 3.727473

mape(data_test$value, for_ctree)

## [1] 4.020834

Slightly better MAPE value with RPART, but again now it can not be anything to generalize. You can read more about CTREE method in its great package vignette. Try to forecast future values with all available electricity load data with sliding window approach (window of the length of three weeks) for a period of more than three months (98 days).

Comparison

Define functions that produce forecasts, so add up everything that we learned so far.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
RpartTrend <- function(data, set_of_date, K, period = 48){
 data_train <- data[date %in% set_of_date]
 
 N <- nrow(data_train)
 window <- (N / period) - 1
 data_ts <- msts(data_train$value, seasonal.periods = c(period, period*7))
 
 fuur <- fourier(data_ts, K = c(K, K))
 fuur_test <- as.data.frame(fourier(data_ts, K = c(K, K), h = period))
 
 data_ts <- ts(data_train$value, freq = period*7)
 decomp_ts <- stl(data_ts, s.window = "periodic", robust = TRUE)
 new_load <- rowSums(decomp_ts$time.series[, c(1,3)])
 trend_part <- ts(decomp_ts$time.series[,2])
 
 trend_fit <- auto.arima(trend_part)
 trend_for <- as.vector(forecast(trend_fit, period)$mean)
 lag_seas <- decomp_ts$time.series[1:(period*window), 1]
 
 matrix_train <- data.table(Load = tail(new_load, window*period),
 fuur[(period+1):N,],
 Lag = lag_seas)
 
 tree_1 <- rpart(Load ~ ., data = matrix_train,
 control = rpart.control(minsplit = 2,
 maxdepth = 30,
 cp = 0.000001))
 test_lag <- decomp_ts$time.series[((period*(window))+1):N, 1]
 
 matrix_test <- data.table(fuur_test,
 Lag = test_lag)
 
 # prediction
 pred_tree <- predict(tree_1, matrix_test) + trend_for
 
 return(as.vector(pred_tree))
}
CtreeTrend <- function(data, set_of_date, K, period = 48){
 
 # subsetting the dataset by dates
 data_train <- data[date %in% set_of_date]
 
 N <- nrow(data_train)
 window <- (N / period) - 1
 data_ts <- msts(data_train$value, seasonal.periods = c(period, period*7))
 
 fuur <- fourier(data_ts, K = c(K, K))
 fuur_test <- as.data.frame(fourier(data_ts, K = c(K, K), h = period))
 
 data_ts <- ts(data_train$value, freq = period*7)
 decomp_ts <- stl(data_ts, s.window = "periodic", robust = TRUE)
 new_load <- rowSums(decomp_ts$time.series[, c(1,3)])
 trend_part <- ts(decomp_ts$time.series[,2])
 
 trend_fit <- auto.arima(trend_part)
 trend_for <- as.vector(forecast(trend_fit, period)$mean)
 lag_seas <- decomp_ts$time.series[1:(period*window), 1]
 
 matrix_train <- data.table(Load = tail(new_load, window*period),
 fuur[(period+1):N,],
 Lag = lag_seas)
 
 tree_2 <- party::ctree(Load ~ ., data = matrix_train,
 controls = party::ctree_control(teststat = "quad",
 testtype = "Teststatistic",
 mincriterion = 0.925,
 minsplit = 1,
 minbucket = 1))
 test_lag <- decomp_ts$time.series[((period*(window))+1):N, 1]
 
 matrix_test <- data.table(fuur_test,
 Lag = test_lag)
 pred_tree <- predict(tree_2, matrix_test) + trend_for
 
 return(as.vector(pred_tree))
}

I created plotly boxplots graph of MAPE values from four models - CTREE simple, CTREE with detrending, RPART simple and RPART with detrending. Whole evaluation can be seen in the script that is stored in my GitHub repository.

We can see that detrending time series of electricity consumption improves the accuracy of the forecast with the combination of both regression tree methods - RPART and CTREE. My approach works as expected.

The habit of my posts is that animation must appear. So, I prepared for you two animations (animated dashboards) using animation, grid, ggplot and ggforce (for zooming) packages that visualize results of forecasting.

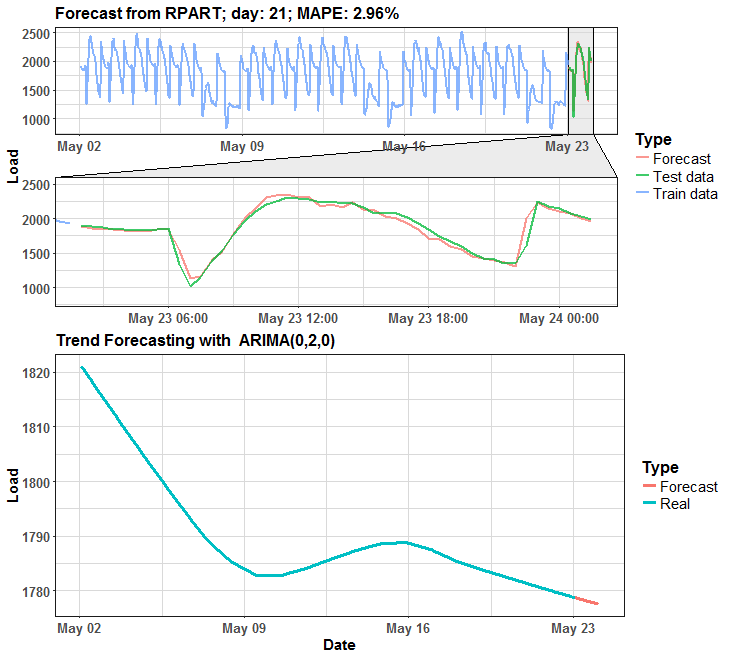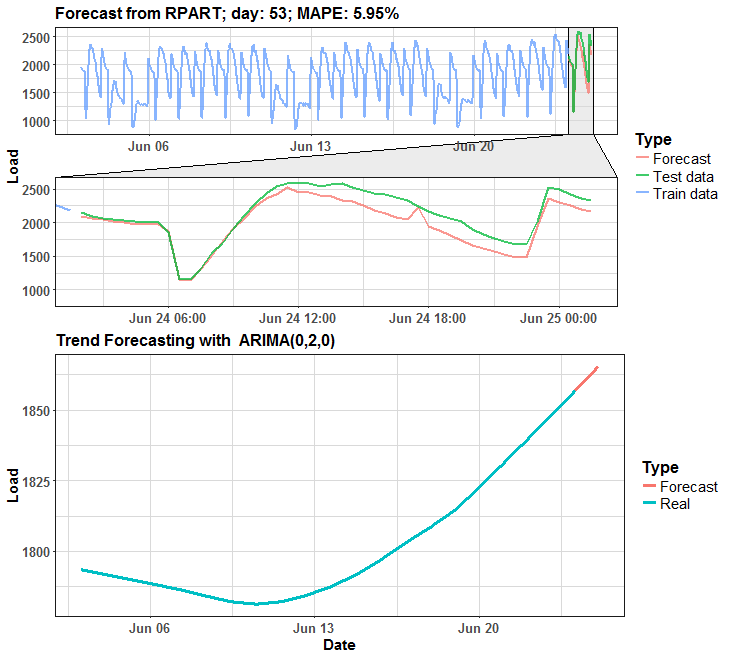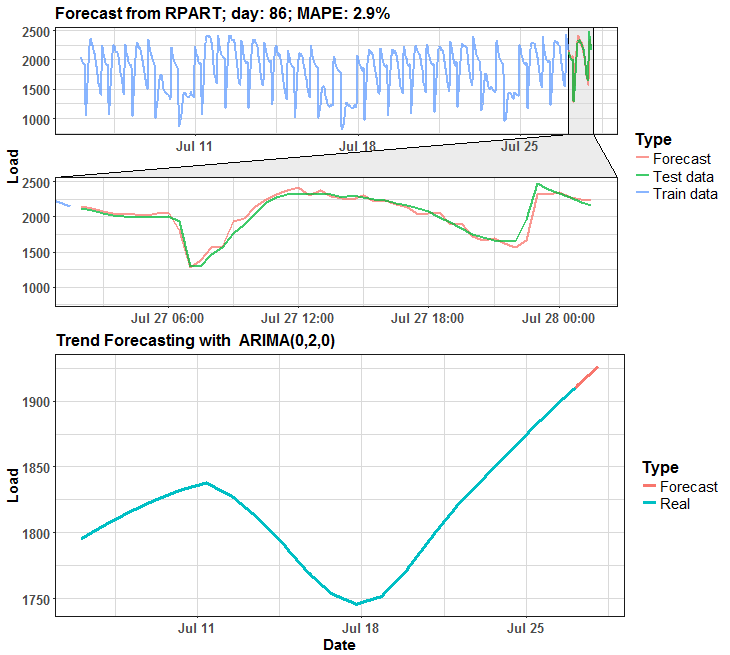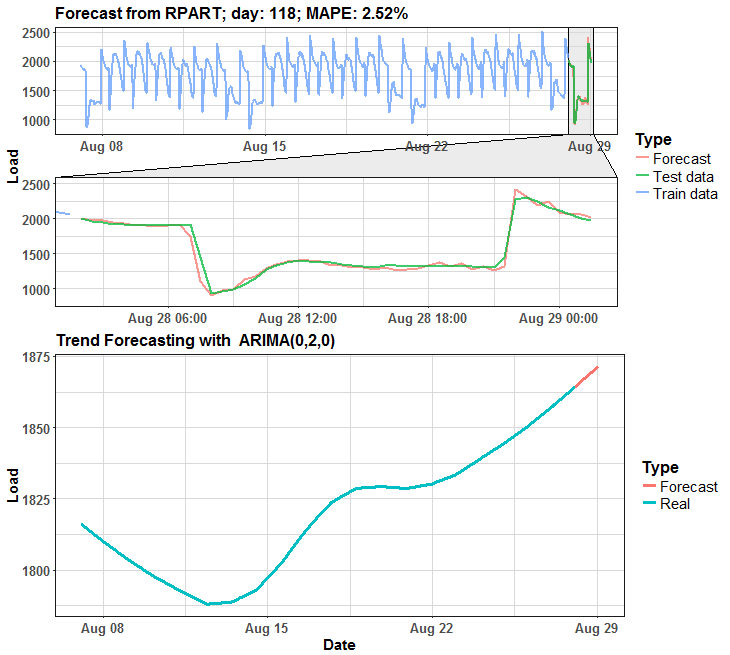
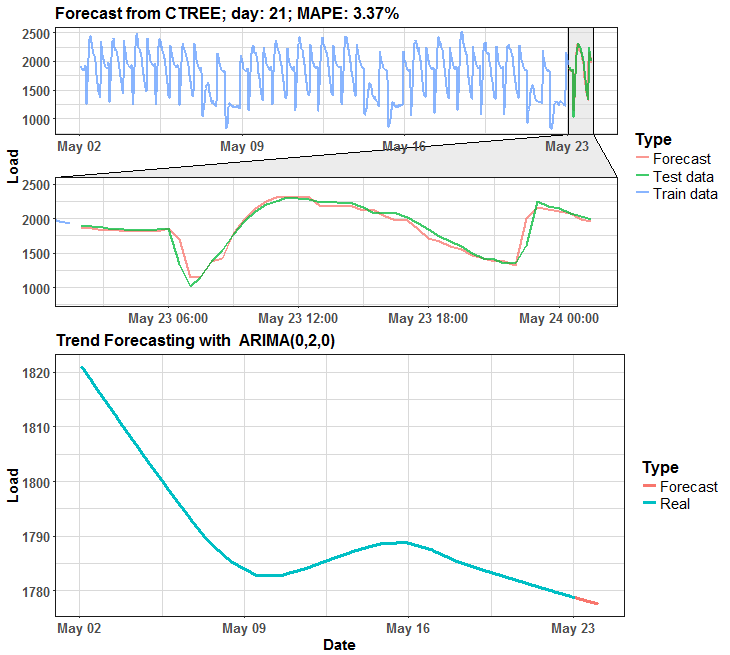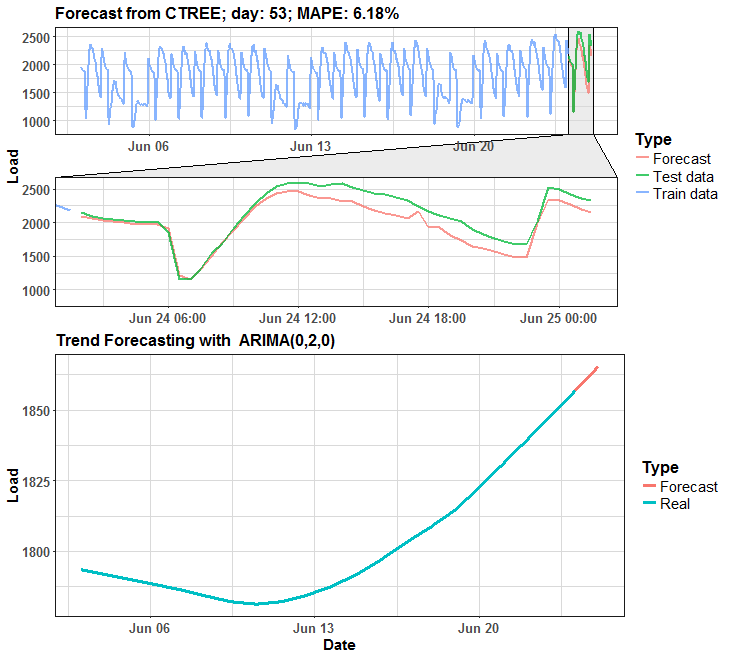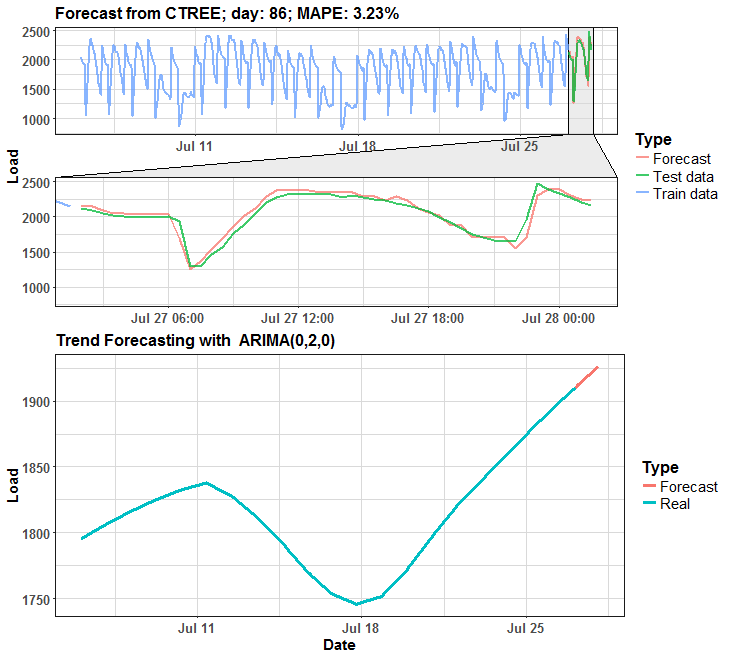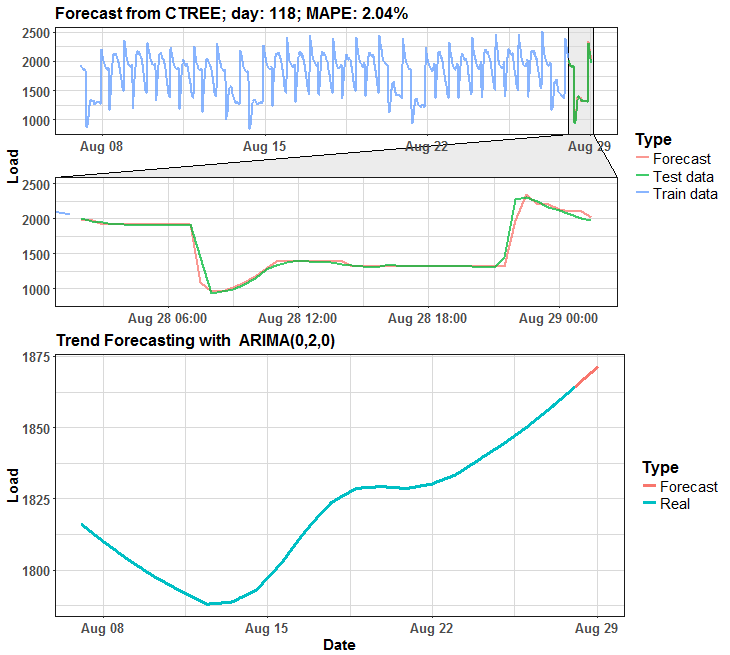
We can see that in many days it is almost perfect forecast, but on some days it has some potential for improving.

Conclusion

In this post, I showed you how to solve trend appearance in seasonal time series with using a regression tree model. Detrending time series for regression tree methods is a important (must) procedure due to the character of decision trees. The trend part of a time series was acquired by STL decomposition and separately forecasted by a simple ARIMA model. I evaluated this approach on the dataset from smart meters measurements of electricity consumption. The regression (decision) tree is a great technique for getting simple and interpretable results in very fast computational time.

In the future post, I will focus on enhancing the predictive performance of simple regression tree methods by ensemble learning methods like Bagging, Random Forest, and similar.