Non-Zero Initial States for Recurrent Neural Networks

The default approach to initializing the state of an RNN is to use a zero state. This often works well, particularly for sequence-to-sequence tasks like language modeling where the proportion of outputs that are significantly impacted by the initial state is small. In some cases, however, it makes sense to (1) train the initial state as a model parameter, (2) use a noisy initial state, or (3) both. This post examines the rationale behind trained and noisy intial states briefly, and presents drop-in Tensorflow implementations.

Training the initial state

If there are enough sequences or state resets in the training data (e.g., this will often be the case if we are doing sequence classification), it may make sense to train the initial state as a variable. This way, the model can learn a good default state. If we have only a few state resets, however, training the initial state as a variable may result in overfitting on the start of each sequence. To see this, consider that with n-step truncated backpropagation, only the first n-steps of each sequence will contribute to the gradient of the initial state, so that even if our single training sequence has one million steps, only thirty of them will be used to train the initial state.

I haven’t seen anyone evaluate this technique (edit 11/22/16: though it appears to be common knowledge), and so I don’t have a good citation for empirical results. Instead, please see the experimental results in this post.

Using a noisy initial state

Using a zero-valued initial state can also result in overfitting, though in a different way. Ordinarily, losses at the early steps of a sequence-to-sequence model (i.e., those immediately after a state reset) will be larger than those at later steps, because there is less history. Thus, their contribution to the gradient during learning will be relatively higher. But if all state resets are associated with a zero-state, the model can (and will) learn how to compensate for precisely this. As the ratio of state resets to total observations increases, the model parameters will become increasingly tuned to this zero state, which may affect performance on later time steps.

One simple solution is to make the initial state noisy. This is the approach suggested by Zimmerman et al. (2012), who take it even a step further by making the magnitude of the initial state noise change according to the backpropagated error. This post will only take the first step of making the initial state noisy.

Tensorflow implementations

In some cases, e.g., as in my post on variable length sequences, creating a variable or noisy initial state to match the cell state is straightforward. However, we often want to switch out the RNN cell or build complicated cells with nested states. My motivation for writing this post was to provide a method like the zero_state method of Tensorflow’s base RNNCell class that automatically constructs a variable or noisy intitial state.

Implementation model

We’ll model the implementation after the zero_state method of Tensorflow’s base RNNCell class, shown below with minor modifications to make it a top-level function. You can view the original zero_state method here.

import numpy as np, tensorflow as tf
from tensorflow.python.util import nest
_state_size_with_prefix = tf.nn.rnn_cell._state_size_with_prefix

def zero_state(cell, batch_size, dtype):
 """Return zero-filled state tensor(s).
 Args:
 cell: RNNCell.
 batch_size: int, float, or unit Tensor representing the batch size.
 dtype: the data type to use for the state.
 Returns:
 If `state_size` is an int or TensorShape, then the return value is a
 `N-D` tensor of shape `[batch_size x state_size]` filled with zeros.
 If `state_size` is a nested list or tuple, then the return value is
 a nested list or tuple (of the same structure) of `2-D` tensors with
 the shapes `[batch_size x s]` for each s in `state_size`.
 """
 state_size = cell.state_size
 if nest.is_sequence(state_size):
 state_size_flat = nest.flatten(state_size)
 zeros_flat = [
 tf.zeros(
 tf.pack(_state_size_with_prefix(s, prefix=[batch_size])),
 dtype=dtype)
 for s in state_size_flat]
 for s, z in zip(state_size_flat, zeros_flat):
 z.set_shape(_state_size_with_prefix(s, prefix=[None]))
 zeros = nest.pack_sequence_as(structure=state_size,
 flat_sequence=zeros_flat)
 else:
 zeros_size = _state_size_with_prefix(state_size, prefix=[batch_size])
 zeros = tf.zeros(tf.pack(zeros_size), dtype=dtype)
 zeros.set_shape(_state_size_with_prefix(state_size, prefix=[None]))

 return zeros

Implementation

Rather than rewriting the zero_state method to initialize the state with a variable (or with noise) directly, we will abstract out the tf.zeros function, to make the method more flexible. Our abstracted function, get_initial_cell_state, takes an additional initializer argument, which takes the place of tf.zeros and determines how the state is initialized. This would be a simple modification, but for the fact that we need to be careful with how variable states are created (e.g., we don’t want a different variable for each sample in the batch), which pushes some of the complexity into the initializer function.

def get_initial_cell_state(cell, initializer, batch_size, dtype):
 """Return state tensor(s), initialized with initializer.
 Args:
 cell: RNNCell.
 batch_size: int, float, or unit Tensor representing the batch size.
 initializer: function with two arguments, shape and dtype, that
 determines how the state is initialized.
 dtype: the data type to use for the state.
 Returns:
 If `state_size` is an int or TensorShape, then the return value is a
 `N-D` tensor of shape `[batch_size x state_size]` initialized
 according to the initializer.
 If `state_size` is a nested list or tuple, then the return value is
 a nested list or tuple (of the same structure) of `2-D` tensors with
 the shapes `[batch_size x s]` for each s in `state_size`.
 """
 state_size = cell.state_size
 if nest.is_sequence(state_size):
 state_size_flat = nest.flatten(state_size)
 init_state_flat = [
 initializer(_state_size_with_prefix(s), batch_size, dtype, i)
 for i, s in enumerate(state_size_flat)]
 init_state = nest.pack_sequence_as(structure=state_size,
 flat_sequence=init_state_flat)
 else:
 init_state_size = _state_size_with_prefix(state_size)
 init_state = initializer(init_state_size, batch_size, dtype, None)

 return init_state

initializer must be a function with four arguments: shape and dtype, a la tf.zeros, and additionally batch_size and index, which are introduced to play nice with variables. We can achieve the same behavior as the original zero_state method with the following initializer function:

def zero_state_initializer(shape, batch_size, dtype, index):
 z = tf.zeros(tf.pack(_state_size_with_prefix(shape, [batch_size])), dtype)
 z.set_shape(_state_size_with_prefix(shape, prefix=[None]))
 return z

Then calling get_initial_cell_state(cell, zero_state_initializer, batch_size, tf.float32) does the same thing as calling zero_state(cell, batch_size, tf.float32).

Given this abstraction, we add support for a variable initializer like so:

def make_variable_state_initializer(**kwargs):
 def variable_state_initializer(shape, batch_size, dtype, index):
 args = kwargs.copy()

 if args.get('name'):
 args['name'] = args['name'] + '_' + str(index)
 else:
 args['name'] = 'init_state_' + str(index)

 args['shape'] = shape
 args['dtype'] = dtype

 var = tf.get_variable(**args)
 var = tf.expand_dims(var, 0)
 var = tf.tile(var, tf.pack([batch_size] + [1] * len(shape)))
 var.set_shape(_state_size_with_prefix(shape, prefix=[None]))
 return var

 return variable_state_initializer

We can now get a variable initial state by calling get_initial_cell_state(cell, make_variable_initializer(), batch_size, tf.float32).

Finally, we can add a noisy wrapper for our zero or variable state intializers like so:

def make_gaussian_state_initializer(initializer, deterministic_tensor=None, stddev=0.3):
 def gaussian_state_initializer(shape, batch_size, dtype, index):
 init_state = initializer(shape, batch_size, dtype, index)
 if deterministic_tensor is not None:
 return tf.cond(deterministic_tensor,
 lambda: init_state,
 lambda: init_state + tf.random_normal(tf.shape(init_state), stddev=stddev))
 else:
 return init_state + tf.random_normal(tf.shape(init_state), stddev=stddev)
 return gaussian_state_initializer

This wrapper adds gaussian noise to the underlying initial_state. E.g., to create an initializer function that initializes the state with a mean of zero and standard deviation of 0.1, we call make_gaussian_state_initializer(zero_state_initializer, stddev=0.01). The deterministic_tensor is an optional boolean tensor that can be used to disable added noise at test time (recommended).

An experiment on the truncated PTB dataset

Now let us test our initializers on a “truncated” PTB language modeling task. This will be the same as the regular PTB dataset, except that we will modify the usual training routine so as to not propagate the final state forward (i.e., it will truncate the state propagation). By reseting the state between each training step, we make the PTB dataset behave like a dataset with many state resets.

Helper functions

from tensorflow.models.rnn.ptb import reader
from enum import Enum

#data from http://www.fit.vutbr.cz/~imikolov/rnnlm/simple-examples.tgz
raw_data = reader.ptb_raw_data('ptb_data')
train_data, val_data, test_data, num_classes = raw_data
batch_size, num_steps = 30, 50

def gen_epochs(n, num_steps, batch_size, dataset=train_data):
 for i in range(n):
 yield reader.ptb_iterator(dataset, batch_size, num_steps)

def reset_graph():
 if 'sess' in globals() and sess:
 sess.close()
 tf.reset_default_graph()

def eval_network(sess, g, num_steps = num_steps, batch_size = batch_size):
 losses = []
 for X, Y in next(gen_epochs(1, num_steps, batch_size, dataset=val_data+test_data)):
 feed_dict={g['x']: X, g['y']: Y, g['deterministic']: True}
 loss_ = sess.run([g['loss']], feed_dict)[0]
 losses.append(loss_)
 return np.mean(losses, axis=0)

def train_network(sess, g, num_epochs, num_steps = num_steps, batch_size = batch_size):
 sess.run(tf.initialize_all_variables())
 losses = []
 val_losses = []
 for idx, epoch in enumerate(gen_epochs(num_epochs, num_steps, batch_size)):
 loss = []
 for X, Y in epoch:
 feed_dict={g['x']: X, g['y']: Y}
 loss_, _ = sess.run([g['loss'], g['train_step']], feed_dict)
 loss.append(loss_)

 val_loss = eval_network(sess, g)
 print("Average perplexity for Epoch", idx,
 ": Training -", np.exp(np.mean(loss)),
 "Validation -", np.exp(np.mean(val_loss)))
 losses.append(np.mean(loss, axis=0))
 val_losses.append(val_loss)
 return np.array(losses), np.array(val_losses)

class StateInitializer(Enum):
 ZERO_STATE = 1
 VARIABLE_STATE = 2
 NOISY_ZERO_STATE = 3
 NOISY_VARIABLE_STATE = 4

Graph

def build_graph(
 state_initializer,
 state_size = 200,
 num_classes = num_classes,
 batch_size = batch_size,
 num_steps = num_steps,
 num_layers = 2):

 reset_graph()

 x = tf.placeholder(tf.int32, [batch_size, num_steps], name='input_placeholder')
 y = tf.placeholder(tf.int32, [batch_size, num_steps], name='labels_placeholder')
 lr = tf.constant(1.)
 deterministic = tf.constant(False)

 embeddings = tf.get_variable('embedding_matrix', [num_classes, state_size])

 rnn_inputs = tf.nn.embedding_lookup(embeddings, x)

 cell = tf.nn.rnn_cell.LSTMCell(state_size, state_is_tuple=True)
 cell = tf.nn.rnn_cell.MultiRNNCell([cell] * num_layers, state_is_tuple=True)

 if state_initializer == StateInitializer.ZERO_STATE:
 initializer = zero_state_initializer
 elif state_initializer == StateInitializer.VARIABLE_STATE:
 initializer = make_variable_state_initializer()
 elif state_initializer == StateInitializer.NOISY_ZERO_STATE:
 initializer = make_gaussian_state_initializer(zero_state_initializer,
 deterministic)
 elif state_initializer == StateInitializer.NOISY_VARIABLE_STATE:
 initializer = make_gaussian_state_initializer(make_variable_state_initializer(),
 deterministic)

 init_state = get_initial_cell_state(cell, initializer, batch_size, tf.float32)
 rnn_outputs, final_state = tf.nn.dynamic_rnn(cell, rnn_inputs, initial_state=init_state)

 with tf.variable_scope('softmax'):
 W = tf.get_variable('W', [state_size, num_classes])
 b = tf.get_variable('b', [num_classes], initializer=tf.constant_initializer(0.0))

 #reshape rnn_outputs and y so we can get the logits in a single matmul
 rnn_outputs = tf.reshape(rnn_outputs, [-1, state_size])
 y_reshaped = tf.reshape(y, [-1])

 logits = tf.matmul(rnn_outputs, W) + b

 losses = tf.reshape(tf.nn.sparse_softmax_cross_entropy_with_logits(logits, y_reshaped),
 [batch_size, num_steps])

 loss_by_timestep = tf.reduce_mean(losses, reduction_indices=0)
 train_step = tf.train.AdamOptimizer().minimize(loss_by_timestep)

 return dict(
 x = x,
 y = y,
 lr = lr,
 deterministic = deterministic,
 init_state = init_state,
 final_state = final_state,
 loss = loss_by_timestep,
 train_step = train_step
 )

Experiment

tr_losses, val_losses = [None] * 4, [None] * 4
g = build_graph(state_initializer=StateInitializer.ZERO_STATE)
sess = tf.InteractiveSession()
tr_losses[0], val_losses[0] = train_network(sess, g, num_epochs=20)

Average perplexity for Epoch 0 : Training - 674.599 Validation - 483.888 Average perplexity for Epoch 1 : Training - 421.366 Validation - 348.751 Average perplexity for Epoch 2 : Training - 305.943 Validation - 272.674 Average perplexity for Epoch 3 : Training - 241.748 Validation - 235.801 Average perplexity for Epoch 4 : Training - 205.29 Validation - 212.853 Average perplexity for Epoch 5 : Training - 180.5 Validation - 198.029 Average perplexity for Epoch 6 : Training - 160.867 Validation - 186.862 Average perplexity for Epoch 7 : Training - 145.657 Validation - 179.394 Average perplexity for Epoch 8 : Training - 133.973 Validation - 173.399 Average perplexity for Epoch 9 : Training - 124.281 Validation - 169.236 Average perplexity for Epoch 10 : Training - 115.586 Validation - 166.216 Average perplexity for Epoch 11 : Training - 108.34 Validation - 163.99 Average perplexity for Epoch 12 : Training - 101.959 Validation - 162.627 Average perplexity for Epoch 13 : Training - 96.3985 Validation - 162.423 Average perplexity for Epoch 14 : Training - 91.6309 Validation - 163.904 Average perplexity for Epoch 15 : Training - 87.29 Validation - 163.679 Average perplexity for Epoch 16 : Training - 83.2224 Validation - 164.169 Average perplexity for Epoch 17 : Training - 79.5156 Validation - 165.162 Average perplexity for Epoch 18 : Training - 76.1198 Validation - 166.714 Average perplexity for Epoch 19 : Training - 73.1628 Validation - 168.515

g = build_graph(state_initializer=StateInitializer.VARIABLE_STATE)
sess = tf.InteractiveSession()
tr_losses[1], val_losses[1] = train_network(sess, g, num_epochs=20)

Average perplexity for Epoch 0 : Training - 525.724 Validation - 325.364 Average perplexity for Epoch 1 : Training - 275.811 Validation - 239.312 Average perplexity for Epoch 2 : Training - 210.521 Validation - 204.103 Average perplexity for Epoch 3 : Training - 176.135 Validation - 184.352 Average perplexity for Epoch 4 : Training - 153.307 Validation - 171.528 Average perplexity for Epoch 5 : Training - 136.591 Validation - 162.493 Average perplexity for Epoch 6 : Training - 123.592 Validation - 156.533 Average perplexity for Epoch 7 : Training - 113.033 Validation - 152.028 Average perplexity for Epoch 8 : Training - 104.201 Validation - 149.743 Average perplexity for Epoch 9 : Training - 96.7272 Validation - 148.263 Average perplexity for Epoch 10 : Training - 90.313 Validation - 147.438 Average perplexity for Epoch 11 : Training - 84.7536 Validation - 147.409 Average perplexity for Epoch 12 : Training - 79.8758 Validation - 147.533 Average perplexity for Epoch 13 : Training - 75.5331 Validation - 148.11 Average perplexity for Epoch 14 : Training - 71.5848 Validation - 149.513 Average perplexity for Epoch 15 : Training - 67.9394 Validation - 151.243 Average perplexity for Epoch 16 : Training - 64.6299 Validation - 153.503 Average perplexity for Epoch 17 : Training - 61.6355 Validation - 156.37 Average perplexity for Epoch 18 : Training - 58.9116 Validation - 160.145 Average perplexity for Epoch 19 : Training - 56.4397 Validation - 164.863

g = build_graph(state_initializer=StateInitializer.NOISY_ZERO_STATE)
sess = tf.InteractiveSession()
tr_losses[2], val_losses[2] = train_network(sess, g, num_epochs=20)

Average perplexity for Epoch 0 : Training - 625.676 Validation - 407.948 Average perplexity for Epoch 1 : Training - 337.045 Validation - 277.074 Average perplexity for Epoch 2 : Training - 245.198 Validation - 230.573 Average perplexity for Epoch 3 : Training - 202.941 Validation - 205.394 Average perplexity for Epoch 4 : Training - 175.752 Validation - 189.294 Average perplexity for Epoch 5 : Training - 156.077 Validation - 178.006 Average perplexity for Epoch 6 : Training - 141.035 Validation - 170.011 Average perplexity for Epoch 7 : Training - 128.985 Validation - 164.033 Average perplexity for Epoch 8 : Training - 118.946 Validation - 160.09 Average perplexity for Epoch 9 : Training - 110.475 Validation - 157.405 Average perplexity for Epoch 10 : Training - 103.191 Validation - 155.624 Average perplexity for Epoch 11 : Training - 96.9187 Validation - 154.584 Average perplexity for Epoch 12 : Training - 91.4146 Validation - 154.25 Average perplexity for Epoch 13 : Training - 86.494 Validation - 154.48 Average perplexity for Epoch 14 : Training - 82.1429 Validation - 155.172 Average perplexity for Epoch 15 : Training - 78.1957 Validation - 156.681 Average perplexity for Epoch 16 : Training - 74.6005 Validation - 158.523 Average perplexity for Epoch 17 : Training - 71.3612 Validation - 160.869 Average perplexity for Epoch 18 : Training - 68.3056 Validation - 163.278 Average perplexity for Epoch 19 : Training - 65.4805 Validation - 165.645

g = build_graph(state_initializer=StateInitializer.NOISY_VARIABLE_STATE)
sess = tf.InteractiveSession()
tr_losses[3], val_losses[3] = train_network(sess, g, num_epochs=20)

Average perplexity for Epoch 0 : Training - 517.27 Validation - 331.341 Average perplexity for Epoch 1 : Training - 278.846 Validation - 239.6 Average perplexity for Epoch 2 : Training - 210.333 Validation - 203.027 Average perplexity for Epoch 3 : Training - 174.959 Validation - 182.456 Average perplexity for Epoch 4 : Training - 151.81 Validation - 169.388 Average perplexity for Epoch 5 : Training - 135.121 Validation - 160.613 Average perplexity for Epoch 6 : Training - 122.301 Validation - 154.474 Average perplexity for Epoch 7 : Training - 111.991 Validation - 150.337 Average perplexity for Epoch 8 : Training - 103.425 Validation - 147.664 Average perplexity for Epoch 9 : Training - 96.1806 Validation - 145.957 Average perplexity for Epoch 10 : Training - 89.8921 Validation - 145.308 Average perplexity for Epoch 11 : Training - 84.3145 Validation - 145.255 Average perplexity for Epoch 12 : Training - 79.3745 Validation - 146.052 Average perplexity for Epoch 13 : Training - 74.96 Validation - 147.01 Average perplexity for Epoch 14 : Training - 71.0005 Validation - 148.22 Average perplexity for Epoch 15 : Training - 67.3658 Validation - 150.713 Average perplexity for Epoch 16 : Training - 64.0655 Validation - 153.78 Average perplexity for Epoch 17 : Training - 61.0874 Validation - 157.101 Average perplexity for Epoch 18 : Training - 58.3892 Validation - 160.376 Average perplexity for Epoch 19 : Training - 55.9478 Validation - 164.157

import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(color_codes=True)

def best_epoch(val_losses):
 return np.argmin(np.mean(val_losses, axis=1))

labels = ['Zero', 'Variable', 'Noisy', 'Noisy Variable']

def plot_losses(losses, title, y_range):
 global val_losses
 fig, ax = plt.subplots()
 for i in range(len(losses)):
 data = np.exp(losses[i][best_epoch(val_losses[i])])
 ax.plot(range(0,num_steps),data,label=labels[i])
 ax.set_xlabel('Step number')
 ax.set_ylabel('Average loss')
 ax.set_ylim(y_range)
 ax.set_title(title)
 ax.legend(loc=1)
 plt.show()

plot_losses(tr_losses, 'Best epoch training perplexities', [70, 110])

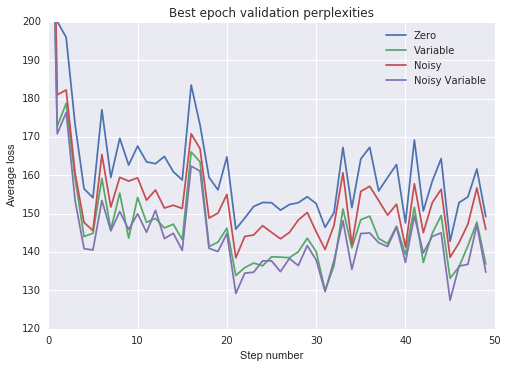
plot_losses(val_losses, ‘Best epoch validation perplexities’, [120, 200]) ```

Empirical results

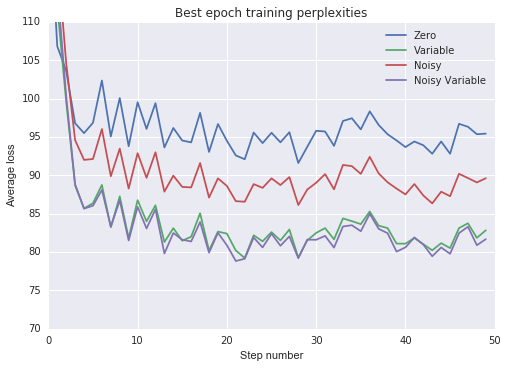
From the above experiment we make the following observations:

All non-zero state intializations sped up training and improved generalization.
Training the initial state as a variable was more effective than using a noisy zero-mean initial state.
Adding noise to a variable initial state provided only marginal benefit.

Finally, I would note that “truncating” the PTB dataset produced worse results than would be obtained if the dataset were not truncated, even if we use noisy or variable state initializations. We can see this by comparing the above results to the “non-regularized LSTM” from Zaremba et al. (2015), which had a very similar architecture, but did not truncate the sequences in the dataset. I would expect truncation will have this effect in general, so that these non-zero state initializations will only really be useful for datasets that have many naturally-occuring state resets.