### Making Deep Networks Probabilistic via Test-time Dropout
In Quantum Mechanics, Heisenberg’s Uncertainty Principle states that there is a fundamental limit to how well one can measure a particle’s position and momentum. In the context of machine learning systems, a similar principle has emerged, but relating interpretability and performance. By using a manually wired or shallow machine learning model, you’ll have no problem understanding the moving pieces, but you will seldom be happy with the results. Or you can use a black-box deep neural network and enjoy the model’s exceptional performance. Today we’ll see one simple and effective trick to make our deep black boxes a bit more intelligible. The trick allows us to convert neural network outputs into probabilities, with no cost to performance, and minimal computational overhead.
The desire to understand deep neural networks has triggered a flurry of research into Neural Network Visualization, but in practice we are often forced to treat deep learning systems as black-boxes. (See my recent Deep Learning Trends @ ICLR 2016 post for an overview of recent neural network visualization techniques.) But just because we can’t grok the inner-workings of our favorite deep models, it doesn’t mean we can’t ask more out of our deep learning systems.
There exists a simple trick for upgrading black-box neural network outputs into probability distributions. The probabilistic approach provides confidences, or “uncertainty” measures, alongside predictions and can make almost any deep learning systems into a smarter one. For robotic applications or any kind of software that must make decisions based on the output of a deep learning system, being able to provide meaningful uncertainties is a true game-changer.
| Applying** Dropout** to your Deep Neural Network is like occasionally zapping your brain |
Without dropout, it is too easy to make a moderately deep network attain 100% accuracy on the training set.
Geoff Hinton’s dropout lecture, also a great introduction, focuses on interpreting dropout as an ensemble method. If you’re looking for new research ideas in the dropout space, a thorough understanding of Hinton’s interpretation is a must.
But while dropout is typically used at training-time, today we’ll highlight the keen observation that dropout used at test-time is one of the simplest ways to turn raw neural network outputs into probability distributions. Not only does this probabilistic “free upgrade” often improve classification results, it provides a meaningful notion of uncertainty, something typically missing in Deep Learning systems. The idea is quite simple: to estimate the predictive mean and predictive uncertainty, simply collect the results of stochastic forward passes through the model using dropout.
How to use dropout: 2016 edition
- Start with a moderately sized network
- Increase your network size with dropout turned off until you perfectly fit your data
- Then, train with dropout turned on
- At test-time, turn on dropout and run the network T times to get T samples
- The mean of the samples is your output and the variance is your measure of uncertainty
Remember that drawing more samples will increase computation time during testing unless you’re clever about re-using partial computations in the network. Please note that if you’re only using dropout near the end of your network, you can reuse most of the computations. If you’re not happy with the uncertainty estimates, consider adding more layers of dropout at test-time. Since you’ll already have a pre-trained network, experimenting with test-time dropout layers is easy.
Bayesian Convolutional Neural Networks To be truly Bayesian about a deep network’s parameters, we wouldn’t learn a single set of parameters w, we would infer a distribution over weights given the data, p(w|X,Y). Training is already quite expensive, requiring large datasets and expensive GPUs. Bayesian learning algorithms can in theory provide much better parameter estimates for ConvNets and I’m sure some of our friends at Google are working on this already. But today we aren’t going to talk about such full Bayesian Deep Learning systems, only systems that “upgrade” the model prediction y to p(y|x,w). In other words, only the network outputs gain a probabilistic interpretation.An excellent deep learning computer vision system which uses test-time dropout comes from a recent University of Cambridge technique called SegNet. The SegNet approach introduced an Encoder-Decoder framework for dense semantic segmentation. More recently, SegNet includes a Bayesian extension that uses dropout at test-time for providing uncertainty estimates. Because the system provides a dense per-pixel labeling, the confidences can be visualized as per-pixel heatmaps. Segmentation system is not performing well? Just look at the confidence heatmaps!
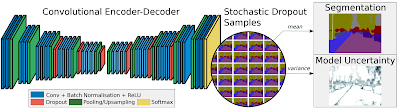 |
Bayesian SegNet. A fully convolutional neural network architecture which provides |Bayesian SegNet. A fully convolutional neural network architecture which provides per-pixel class uncertainty estimates using dropout.|
Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding Alex Kendall, Vijay Badrinarayanan, Roberto Cipolla, in arXiv:1511.02680, November 2015. [project page with videos]
### Theoretical Bayesian Deep Learning
 |
The Gaussian Process: A machine learning approach with built-in uncertainty modeling
###
 |
| The Gaussian Process: A machine learning approach with built-in uncertainty modeling |
Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning Yarin Gal, Zoubin Ghahramani, in ICML. June 2016. [Appendix with relationship to Gaussian Processes]A Theoretically Grounded Application of Dropout in Recurrent Neural Networks Yarin Gal, in arXiv:1512.05287. May 2016.
I do wonder what Yann LeCun thinks about Bayesian ConvNets… Last I heard, he was allergic to sampling.
Related Posts Deep Learning vs Probabilistic Graphical Models vs Logic April 2015Deep Learning Trends @ ICLR 2016 June 2016