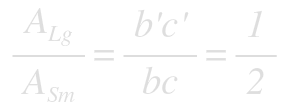
The law of cosines provides us a nice expression for the length of the cut(L), in terms of b’ and c’:
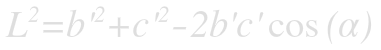
Using the ratio of the areas to find an expression for b’, we can write L in terms of a single variable, c’:
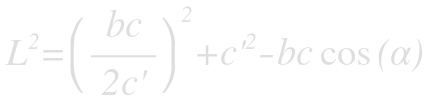
To minimize the cut length for a certain angle α, take the derviative of L with respect to c’:
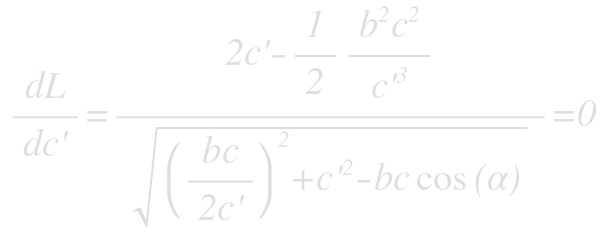
Fortunately, only the numerator must be zero. Solving the numerator for c’ yields
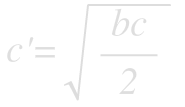
which, using the relationship from the area ratios gives.
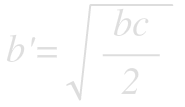
Result
What we find in the end is that the shortest cut of an arbitrary triangle comes when you cut off an isosceles triangle of equal area. This is a natural generalization of the result from the equilateral cake. In that case, we cut an isosceles triangle that happened to have the third side equal to the other two, making it equilateral.
Cut Length
Using these equations we can determine the length of the smallest cut by substitution to find:
This is super pretty! Checking in with the equilateral triangle (α=60°, b=c=1) we recover the correct value of 1/√2. However, it would be nice to express the length solely in terms of the cake dimensions. This is possible using our good friend the law of cosines to determine cos(α) in terms of a, b, and c. The result is the rather find looking expression:
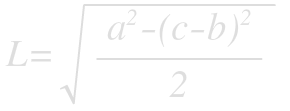
| Thanks for indulging me in a bit of mathematical fun. Next time you and a buddy order a triangle cake that comes out quite scalene, you now can split it evenly. All this cake talk has made me hungry… |
You can find a complete list of all the articles here.
Click here to receive email alerts on new articles.