There’s a famous quote from former Secretary of Defense Donald Rumsfeld:
“ … there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns – the ones we don’t know we don’t know.”
 |
I write this blog. I’m an engineer. Whilst I do my best and try to proof read, often mistakes creep in. I know there are probably mistakes in just about everything I write! How would I go about estimating the number of errors?The idea for this article came from a book I recently read by Paul J. Nahin, entitled Duelling Idiots and Other Probability Puzzlers (In turn, referencing earlier work by the eminent mathematician George Pólya). |
The idea for this article came from a book I recently read by Paul J. Nahin, entitled Duelling Idiots and Other Probability Puzzlers (In turn, referencing earlier work by the eminent mathematician George Pólya).
Proof Reading2
Imagine I write a (non-trivially short) document and give it to two proof readers to check. These two readers (independantly) proof read the manuscript looking for errors, highlighting each one they find.
Just like me, these proof readers are not perfect. They, also, are not going to find all the errors in the document.
Because they work independently, there is a chance that reader #1 will find some errors that reader #2 does not (and vice versa), and there could be errors that are found by both readers. What we are trying to do is get an estimate for the number of unseen errors (errors detected by neither of the proof readers).*
An alternate way of thinking of this is to get an estimate for the *total number of errors in the document (from which we can subtract the distinct number of errors found to give an estimate to the number of unseen errros.
Definitions
We’re going to asume that the proofers only find (or don’t find) actual errors in the document. We’re ignoring the possibility of a false-positive responses (where a proofer indentifies a mistake that is not really a mistake).
Let’s define some variables:
-
n is the actual number of errors in the manuscript (total).
-
n1 is the number of errors found by reader #1.
-
n2 is the number of errors found by reader #2.
-
b is the number of errors found by both proof readers.
-
u is the number of unseen errors (the number we are trying to estimate).
Thought experiments
If the number of errors found by both readers is high (with a relatively small number found distinctly independant), then there is a good chance that there are not many unfound errors (A high correlation between the found errors indicates that most have been found).
Similarly, if there is a ‘good’ proofer (someone who has great skill and finds errors with high probability), this would suggest that the errors s(he) found is close to the actual number, and by comparing to the other proof reader we can estimate how ‘good’ they are by the number found by the second not found by the first.
Interestingly, as we will see, we can make an estimate about the number of unseen errors based purely on the count of the errors, and this estimate is agnostic of the skill of either of the proof readers, and independent of the document length!
|
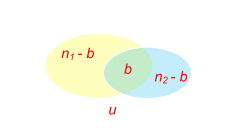|There is a simple relationship between all the errors from basic set theory:n = u n1 n2 − b|
This makes total sense. The total number of the errors in the document is equal to the number of unfound errors, plus the number found by each proofer, subtract the number found by both (we don’t want to double count).
Next we need to examine how the proofers find the errors. Below is a digram showing all the errors in the manuscript. We make the assumption that there is an fixed independent probability of each proofer finding an error.
For the first reader, this is probability P1. For the second reader, this is probability P2.
Mathematicians call these Bernoulli Trials. The error is found, or it is not. The probability that any one error is found is found by the first proofer is P1, the probability that it is not found is (1 − P1).
These probabilities are equal to the number of errors found over the total number of errors that could be found.
P1 = n1/n P2 = n2/n
And since the proofers read independatly, the chances of them finding both is logical AND (we multiply probabilities)
P1P2 = b/n
These Bernoulli trials will have a binomial distribution and (for n>0) the expected number of errors can be given by the formula:
n = (nP1)(nP2) / (nP1P2)